题目内容
 (2012•南昌)如图,已知两个菱形ABCD、CEFG,其中点A、C、F在同一直线上,连接BE、DG.
(2012•南昌)如图,已知两个菱形ABCD、CEFG,其中点A、C、F在同一直线上,连接BE、DG.(1)在不添加辅助线时,写出其中的两对全等三角形;
(2)证明:BE=DG.
分析:(1)△ADC≌△ABC,△GFC≌△EFC,根据菱形的性质推出AD=AB,DC=BC,根据SSS即可证出结论;
(2)根据菱形性质求出DC=BC,CG=CE,推出∠DCG=∠BCE,根据SAS证出△DCG≌△BCE即可.
(2)根据菱形性质求出DC=BC,CG=CE,推出∠DCG=∠BCE,根据SAS证出△DCG≌△BCE即可.
解答:(1)解:△ADC≌△ABC,△GFC≌△EFC;
(2)证明:∵四边形ABCD、CEFG是菱形,
∴DC=BC,CG=CE,∠DCA=∠BCA,∠GCF=∠ECF,
∵∠ACF=180°,
∴∠DCG=∠BCE,
在△DCG和△BCE中
∵
,
∴△DCG≌△BCE,
∴BE=DG.
(2)证明:∵四边形ABCD、CEFG是菱形,
∴DC=BC,CG=CE,∠DCA=∠BCA,∠GCF=∠ECF,
∵∠ACF=180°,
∴∠DCG=∠BCE,
在△DCG和△BCE中
∵
|
∴△DCG≌△BCE,
∴BE=DG.
点评:本题考查了菱形的性质和全等三角形的性质和判定的应用,注意:菱形的四条边都相等,且每一条对角线平分一组对角.

练习册系列答案
相关题目
 (2012•南昌)如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,
(2012•南昌)如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时, (2012•南昌)如图,有a、b、c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线( )
(2012•南昌)如图,有a、b、c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线( ) (2012•南昌)如图,如果在阳光下你的身影的方向北偏东60°方向,那么太阳相对于你的方向是( )
(2012•南昌)如图,如果在阳光下你的身影的方向北偏东60°方向,那么太阳相对于你的方向是( )
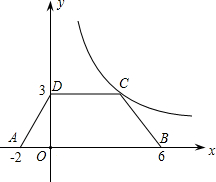 (2012•南昌)如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(2012•南昌)如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.