题目内容
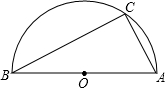
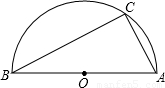
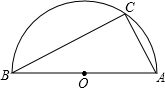
已知如图，AB为半圆⊙O的直径，C为半圆上的一点．
（1）请你只用直尺和圆规，分别以AC、BC为直径，向△ABC外侧作半圆．（不必写出作法，只需保留作图痕迹）
（2）若AC=3，BC=4，求所作的两个半圆中不与⊙O重叠的部分的面积和．
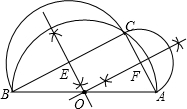
解：（1）如图：
（2）设以BC为直径的半圆与已知半圆不重合的部分面积为S1，重合部分面积为S2，
以AC为直径的半圆与已知半圆不重合的部分面积为S3，重合部分面积为S4，
则∵AB为直径，∴∠C=90°，又∵AC=3，BC=4，∴AB=5
∵S1+S2=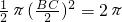
，
S3+S4=
，
S2+S4+S△ABC=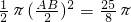
，
∴S1+S2+S3+S4=S2+S4+S△ABC，
∴S1+S3=S△ABC=6．
分析：（1）作BC的中垂线交于BC于点E，以点E为圆心，BE为半径作半圆，作AC的中垂线交于AC于点F，以点F为圆心，AF为半径作半圆；
（2）由勾股定理知，以AB为直径的半圆的面积等于以BC为直径的半圆的面积与以AC为直径的半圆与以AC为直径的半圆的面积的和，建立方程，即可求得两个半圆中不与⊙O重叠的部分的面积和．
点评：本题利用了中垂线的作法，和勾股定理，半圆的面积公式求解．
（2）设以BC为直径的半圆与已知半圆不重合的部分面积为S1，重合部分面积为S2，
以AC为直径的半圆与已知半圆不重合的部分面积为S3，重合部分面积为S4，
则∵AB为直径，∴∠C=90°，又∵AC=3，BC=4，∴AB=5
∵S1+S2=
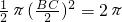，S3+S4=
，S2+S4+S△ABC=
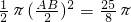，∴S1+S2+S3+S4=S2+S4+S△ABC，
∴S1+S3=S△ABC=6．
分析：（1）作BC的中垂线交于BC于点E，以点E为圆心，BE为半径作半圆，作AC的中垂线交于AC于点F，以点F为圆心，AF为半径作半圆；
（2）由勾股定理知，以AB为直径的半圆的面积等于以BC为直径的半圆的面积与以AC为直径的半圆与以AC为直径的半圆的面积的和，建立方程，即可求得两个半圆中不与⊙O重叠的部分的面积和．
点评：本题利用了中垂线的作法，和勾股定理，半圆的面积公式求解．
练习册系列答案
特高级教师点拨系列答案
相关题目
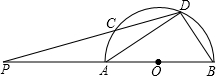已知如图，AB为半圆的直径，C、D为半圆弧上的两点，若弧CD=弧BD，DC与BA的延长线交于P，如果，AP：CP=3：4，△ADB的面积为
