题目内容
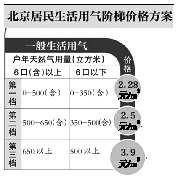
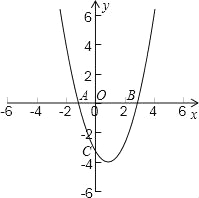
【题目】在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与x轴的负半轴相交于点C(如图),点C的坐标为(0,﹣3),且BO=CO
(1)求这个二次函数的解析式;
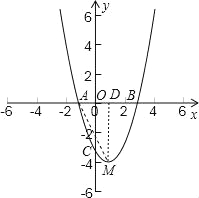
(2)设这个二次函数的图象的顶点为M,求AM的长.
【答案】(1)y=x2﹣2x﹣3;
(2)AM=![]() =
=![]() =2
=2![]() .
.
【解析】
试题分析:(1)由已知可得B(3,0),又C(0,﹣3),代入抛物线解析式可求b、c;
(2)求抛物线顶点坐标,设对称轴与x轴交于D点,在直角三角形中用勾股定理可求AM的长.
试题解析:(1)∵C(0,﹣3),OC=|﹣3|=3,∴c=﹣3,又∵OC=BO,∴BO=3,∴B(3,0)
9+3b﹣3=0,6+3b=0,b=﹣2,∴y=x2﹣2x﹣3;
(2)∵对称轴x=![]() ,B(3,0),∴A点坐标为:(﹣1,0),
,B(3,0),∴A点坐标为:(﹣1,0),
∵顶点纵坐标y=﹣4,∴AM=![]() =
=![]() =2
=2![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目