题目内容
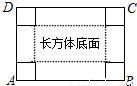
如图,小明把一张矩形的硬纸板ABCD的四周各剪去一个边长为x(cm)的小正方形,再折合成一个无盖的长方体盒子,AB=14cm,AD=10cm.(1)如果长方体的底面面积为60cm2,则x的值是多少?
(2)求长方体的底面周长y(cm)的取值范围.
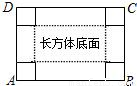
【答案】分析:(1)减去一个边长为x的小正方形,长方形底面的长就为(14-2x),宽为(10-2x),根据底面面积为60,可列方程求解.
(2)长方形的周长为y=2(10-2x)+2(14-2x)=48-8x,可见y随x的增大而减小.
解答:解:(1)列出方程:(10-2x)(14-2x)=60
化简:4x2-48x+140=60即x2-12x+20=0
解出x1=2,x2=10(不合题意舍去)
答:x的值是2cm.
(2)y=2(10-2x)+2(14-2x)=48-8x,
列出不等式组:
10-2x>0
14-2x>0
解得0<x<5
∵y随x增大而减小,x=5时,y=8;x=0时,y=48
∴y的取值范围是:8<y<48
点评:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题的第一问关键是表示出长和宽.第二问能找到y和x的关系式,然后根据x的取值范围进行讨论.
(2)长方形的周长为y=2(10-2x)+2(14-2x)=48-8x,可见y随x的增大而减小.
解答:解:(1)列出方程:(10-2x)(14-2x)=60
化简:4x2-48x+140=60即x2-12x+20=0
解出x1=2,x2=10(不合题意舍去)
答:x的值是2cm.
(2)y=2(10-2x)+2(14-2x)=48-8x,
列出不等式组:
10-2x>0
14-2x>0
解得0<x<5
∵y随x增大而减小,x=5时,y=8;x=0时,y=48
∴y的取值范围是:8<y<48
点评:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题的第一问关键是表示出长和宽.第二问能找到y和x的关系式,然后根据x的取值范围进行讨论.

练习册系列答案
相关题目
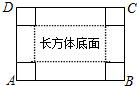 22、如图,小明把一张矩形的硬纸板ABCD的四周各剪去一个边长为x(cm)的小正方形,再折合成一个无盖的长方体盒子,AB=14cm,AD=10cm.
22、如图,小明把一张矩形的硬纸板ABCD的四周各剪去一个边长为x(cm)的小正方形,再折合成一个无盖的长方体盒子,AB=14cm,AD=10cm.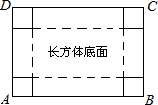 (2011•同安区模拟)如图,小明把一张矩形的硬纸板ABCD的四周各剪去一个边长为x(cm)的小正方形,再折合成一个无盖的长方体盒子,已知:AB=12cm,AD=10cm.请填写下表
(2011•同安区模拟)如图,小明把一张矩形的硬纸板ABCD的四周各剪去一个边长为x(cm)的小正方形,再折合成一个无盖的长方体盒子,已知:AB=12cm,AD=10cm.请填写下表 如图,小明把一张矩形的硬纸板ABCD的四周各剪去一个边长为x(cm)的小正方形,再折合成一个无盖的长方体盒子,AB=14cm,AD=10cm.
如图,小明把一张矩形的硬纸板ABCD的四周各剪去一个边长为x(cm)的小正方形,再折合成一个无盖的长方体盒子,AB=14cm,AD=10cm.