题目内容
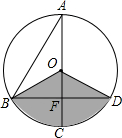 如图,在⊙O中,AB=
如图,在⊙O中,AB=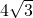 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°,若用阴影扇形OBD围成一个圆锥侧面,则这个圆锥的底面半径是________.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°,若用阴影扇形OBD围成一个圆锥侧面,则这个圆锥的底面半径是________.

分析:先利用同弧所对的圆周角等于所对的圆心角的一半,求出扇形的圆心角为120度,直接根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得圆锥的底面圆的半径.
解答:
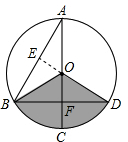 解:过O作OE⊥AB于E,则
解:过O作OE⊥AB于E,则AE=
 AB=2
AB=2 .
.在Rt△AEO中,∠BAC=30°,cos30°=
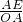 .
.∴OA=
 =
=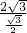 =4.
=4.又∵OA=OB,
∴∠ABO=30°.
∴∠BOC=60°.
∵AC⊥BD,
∴
 =
=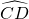 .
.∴∠COD=∠BOC=60°.
∴∠BOD=120°.
设圆锥的底面圆的半径为r,则周长为2πr,
∴2πr=
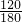 π•4.
π•4.∴r=
 .
.故答案为:
 .
.点评:本题主要考查了圆锥的侧面展开图与底面周长之间的关系.本题还涉及到圆中的一些性质,如垂径定理等.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G. 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.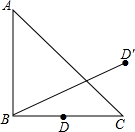 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′= 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有