Question

【题目】如图,是的直径,交于,是上一点,为内心,交于,且.

(1)求证:是的切线;

(2)求证:.

Answer 1

【答案】见解析

【解析】

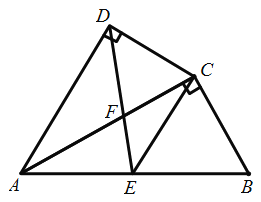
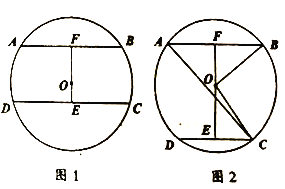
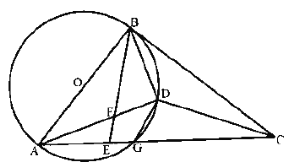
（1）利用三角形内心性质得∠EBD＝∠CBD．加上∠DBE＝∠BAD，则∠CBD＝∠BAD，根据圆周角定理得到∠BDA＝90°．然后证明∠ABC＝90°．于是根据切线的判定定理可判断BC是⊙O的切线；

（2）连接ED，如图，则∠BED＝∠CED，再证明∠EFD＝∠EGD，从而可判断△DFE≌△DGE．于是得到DF＝DG．

（1）∵点D为△BCE的内心，

∴BD平分∠EBC．

∴∠EBD＝∠CBD．

又∵∠DBE＝∠BAD，

∴∠CBD＝∠BAD．

又∵AB是〇O直径，

∴∠BDA＝90°．

在Rt△BAD中，∠BAD＋∠ABD＝90°，

∴∠CBD＋∠ABD＝90°，即∠ABC＝90°．

∴BC⊥AB．

又∵AB为直径，

∴BC是〇O的切线；

（2）连接ED，如图，

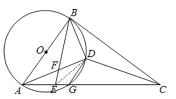
则ED平分∠BEC，

∴∠BED＝∠CED．

∵∠EFD为△BFD的外角

∴∠EFD＝∠ADB＋∠EBD＝90°＋∠EBD，

又∵四边形ABDG为圆的内接四边形，

∴∠EGD＝180°∠ABD＝180°（90°∠CBD）＝90°＋∠CBD，

又∵∠EBD＝∠CBD，

∴∠EFD＝∠EGD

又∵ED＝ED，

∴△DFE≌△DGE（AAS ）．

∴DF＝DG．