题目内容
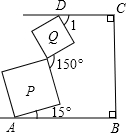 如图,正方形P、Q夹在ABCD框架中,正方形P下边一条边与AB夹角为15°,正方形P、Q有两个相邻边夹角为150°,则∠1为
如图,正方形P、Q夹在ABCD框架中,正方形P下边一条边与AB夹角为15°,正方形P、Q有两个相邻边夹角为150°,则∠1为
- A.55°
- B.15°
- C.50°
- D.70°
B
分析:延长正方形P、Q的边相交于点E(点E如果不在BC上,可以过E作BC的平行线),根据四边形的内角和等于360°求出∠AED的度数为30°,又∠1+∠EAB=∠AED,代入数据计算即可求出∠1的度数.
解答: 解:如图,延长正方形P、Q的边相交于点E,过E作BC的平行线,过E作EM∥AB,
解:如图,延长正方形P、Q的边相交于点E,过E作BC的平行线,过E作EM∥AB,
则∠AED=360°-150°-90°-90°=30°,
∵∠AED=∠1+∠EAG,
∴∠1=∠AED-∠EAG=30°-15°=15°.
故选B.
点评:本题利用正方形的四个角都是直角,直角的邻补角也是直角,四边形的内角和定理和两直线平行,内错角相等的性质,延长正方形的边构造四边形是解题的关键.
分析:延长正方形P、Q的边相交于点E(点E如果不在BC上,可以过E作BC的平行线),根据四边形的内角和等于360°求出∠AED的度数为30°,又∠1+∠EAB=∠AED,代入数据计算即可求出∠1的度数.
解答:
 解:如图,延长正方形P、Q的边相交于点E,过E作BC的平行线,过E作EM∥AB,
解:如图,延长正方形P、Q的边相交于点E,过E作BC的平行线,过E作EM∥AB,则∠AED=360°-150°-90°-90°=30°,
∵∠AED=∠1+∠EAG,
∴∠1=∠AED-∠EAG=30°-15°=15°.
故选B.
点评:本题利用正方形的四个角都是直角,直角的邻补角也是直角,四边形的内角和定理和两直线平行,内错角相等的性质,延长正方形的边构造四边形是解题的关键.

练习册系列答案
相关题目
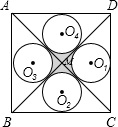 如图,正方形ABCD的对角线AC、BD交于点M,且分正方形为四个三角形,⊙O1、⊙O2、⊙O3、⊙O4分别为△AMB、△BMC、△CMD、△DMA的内切圆,已知AB=1.则⊙O1、⊙O2、⊙O3、⊙O4.所夹的中心(阴影)部分的面积为( )
如图,正方形ABCD的对角线AC、BD交于点M,且分正方形为四个三角形,⊙O1、⊙O2、⊙O3、⊙O4分别为△AMB、△BMC、△CMD、△DMA的内切圆,已知AB=1.则⊙O1、⊙O2、⊙O3、⊙O4.所夹的中心(阴影)部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
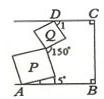 10、如图,正方形P、Q夹在ABCD框架中,正方形P下边一条边与AB夹角为15°,正方形P、Q有两个相邻边夹角为150°,则∠1为( )
10、如图,正方形P、Q夹在ABCD框架中,正方形P下边一条边与AB夹角为15°,正方形P、Q有两个相邻边夹角为150°,则∠1为( ) 如图,正方形ABCD的对角线AC、BD交于点M,且分正方形为四个三角形,⊙O1、⊙O2、⊙O3、⊙O4分别为△AMB、△BMC、△CMD、△DMA的内切圆,已知AB=1.则⊙O1、⊙O2、⊙O3、⊙O4.所夹的中心(阴影)部分的面积为
如图,正方形ABCD的对角线AC、BD交于点M,且分正方形为四个三角形,⊙O1、⊙O2、⊙O3、⊙O4分别为△AMB、△BMC、△CMD、△DMA的内切圆,已知AB=1.则⊙O1、⊙O2、⊙O3、⊙O4.所夹的中心(阴影)部分的面积为







