Question

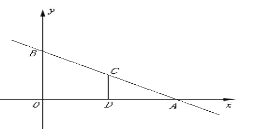
【题目】如图,平面直角坐标系中,直线AB与轴,轴分别交于A(3,0),B(0,)两点, ,点C为线段AB上的一动点,过点C作CD⊥轴于点D.

(1)求直线AB的解析式;

(2)若S梯形OBCD＝,求点C的坐标;

Answer 1

【答案】（1）y=-x+；（2）C（2，）.

【解析】

试题分析：（1）直线AB解析式为：y=kx+b，把A，B的坐标代入代入然后解方程组即可；（2）设点C坐标为（x，- x+），然后用x表示出S梯形OBCD，得出方程，解方程即可.

试题解析：（1）设直线AB解析式为：y=kx+b，

把A，B的坐标代入得：k=﹣，b=，

所以直线AB的解析为：y=-x+；

（2）设点C坐标为（x，- x+），

那么OD=x，CD=-x+．

∴S梯形OBCD=．

由题意得：，

解得：x1=2，x2=4（舍去），

∴C（2，）.