题目内容
在河道L旁有两个村庄A、B,两村相距1000米,且A村与河道的距离为100米,B村到河道距离为700米,若要在河道上修建一个供水站,要使它到两村的距离之和最短,则最短距离为( )
A.800
| B.1000 | C.800 | D.800
|
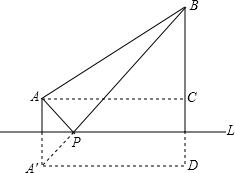
如图所示,当A,B村在河道同侧时,
∵A村与河道的距离为100米,B村到河道距离为700米,A、B两村相距1000米,
∴AB=1000,BC=700-100=600,
根据勾股定理,AC=
=
=800(米),
作点A关于河岸的对称点A′,连接A′B与河岸相交于点P,根据轴对称确定最短路线问题,
点P即为修建供水站的地方,
作AD∥L交B村与河岸的垂线于D,
则A′D=AC=800米,
BD=700+100=800米,
根据勾股定理,A′B=
=
=800
(米),
即最短距离为800
m.
当A,B村在河道异侧时,
AB=1000m,则最短距离为1000m.
故选D.
∵A村与河道的距离为100米,B村到河道距离为700米,A、B两村相距1000米,
∴AB=1000,BC=700-100=600,
根据勾股定理,AC=
| AB2-BC2 |
| 10002-6002 |
作点A关于河岸的对称点A′,连接A′B与河岸相交于点P,根据轴对称确定最短路线问题,
点P即为修建供水站的地方,
作AD∥L交B村与河岸的垂线于D,
则A′D=AC=800米,
BD=700+100=800米,
根据勾股定理,A′B=
| A′D2+BD2 |
| 8002+8002 |
| 2 |
即最短距离为800
| 2 |
当A,B村在河道异侧时,
AB=1000m,则最短距离为1000m.
故选D.


练习册系列答案
相关题目