Question

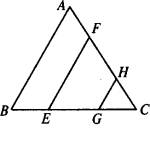
　　如图，在△ABC中，EF∥CD，DE∥BC，求证：AF∶FD＝AD∶DB．

 

Answer 1

答案：
解析：

证明：在△ACD中， 　　∵EF∥CD，∴. 　　在△ACB中，∵ED∥CB，∴. 　　由①②得，AF∶FD＝AD∶DB． 　　说明：证明比例式时，往往要寻找中间比，以沟通待证式的左右两边，中间比是纽带与桥梁．

提示：

导析：本题已知两组直线平行，求证一个比例式，这个比例式的左边线段的比是指在△ACD中被EF所截的两条线段的比．这个比例式的右边是△ACB中被ED所截的两条线段的比．左右两边的比要相等，就要找一个中间比是AE∶EC．