题目内容
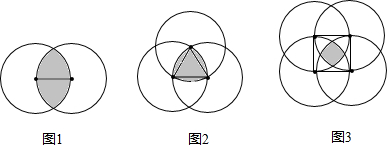
宏远广告公司要为某企业的一种产品设计商标图案,给出了如下几种初步方案,供继续设计选用(设图中圆的半径均为r)(1)如图1,分别以线段O1O2的两个端点为圆心,以这条线段的长为半径作出两个互相交错的圆的图案,试求两圆相交部分的面积;
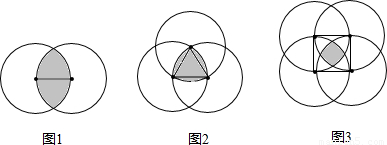
(2)如图2,分别以等边△O1O2O3的三个顶点为圆心,以其边长为半径,作出三个两两相交的相同的圆,这时,这三个圆相交部分的面积又是多少呢?
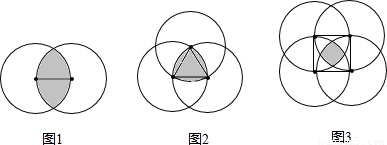
(3)如图3,分别以正方形O1O2O3O4的四个顶点为圆心,以其边长为半径,作出四个相同的圆,这时,这四个圆相交部分的面积又是多少呢?
【答案】分析:(1)设两圆交于A,B两点,连接O1A,O2A,O1B,O2B.
求两圆相交部分的面积,即求S菱形+4S弓的面积.由题意知△O1O2A为正三角形,四个弓形的圆心角为60°,分别求出求S菱形,及弓形的面积即可;
(2)求三个圆相交部分的面积,即求S△O1O2A+3S弓.由题意知△O1O2A为正三角形,三个弓形的圆心角为60°,分别求△O1O2O3的面积,及弓形的面积即可;
(3)要求四个圆相交部分的面积,即求S正方形-4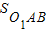 ,而
,而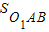 =
=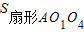 -
-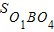 ,由(1)可求
,由(1)可求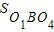 .
.
解答:解:(1)设两圆交于A,B两点,连接O1A,O2A,O1B,O2B.
则S阴=S菱形+4S弓.
∵S菱形=2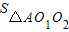 ,△O1O2A为正三角形,其边长为r.
,△O1O2A为正三角形,其边长为r.
∴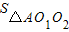 =
=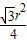 ,S弓=
,S弓=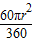 -
-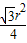 =
=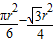 .
.
∴S阴=2×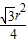 +4(
+4(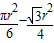 )=
)= πr2-
πr2-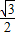 r2.
r2.
(2)图2阴影部分的面积为:
S阴=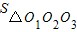 +3S弓
+3S弓
∵△O1O2O3为正三角形,边长为r,
∴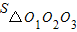 =
=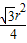 .
.
∴S弓=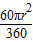 -
-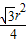 .
.
S阴=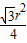 +3(
+3(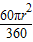 -
-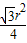 )=
)=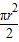
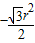 .
.
(3)延长O2O1与⊙O1交于点A,⊙O1与⊙O4交于点B.
由(1)知,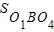 =
= (
(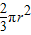 -
-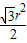 ).
).
∵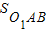 =
=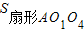 -
-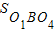 =
=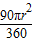 -
- (
(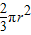 -
- )=
)=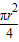
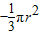 +
+ ,
,
则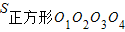 -4
-4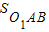 =r2-4(
=r2-4(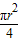
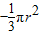 +
+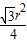 )=(
)=(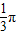 +1-
+1-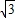 )r2.
)r2.
点评:本题难度较大,考查圆与圆的位置关系中,互相交错的圆的图案的面积问题,同时考查了综合应用能力及推理能力.
求两圆相交部分的面积,即求S菱形+4S弓的面积.由题意知△O1O2A为正三角形,四个弓形的圆心角为60°,分别求出求S菱形,及弓形的面积即可;
(2)求三个圆相交部分的面积,即求S△O1O2A+3S弓.由题意知△O1O2A为正三角形,三个弓形的圆心角为60°,分别求△O1O2O3的面积,及弓形的面积即可;
(3)要求四个圆相交部分的面积,即求S正方形-4
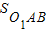 ,而
,而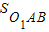 =
=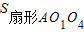 -
-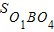 ,由(1)可求
,由(1)可求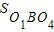 .
.解答:解:(1)设两圆交于A,B两点,连接O1A,O2A,O1B,O2B.
则S阴=S菱形+4S弓.
∵S菱形=2
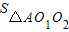 ,△O1O2A为正三角形,其边长为r.
,△O1O2A为正三角形,其边长为r.∴
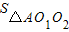 =
=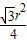 ,S弓=
,S弓=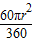 -
-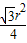 =
=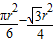 .
.∴S阴=2×
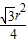 +4(
+4(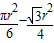 )=
)= πr2-
πr2-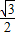 r2.
r2.
(2)图2阴影部分的面积为:
S阴=
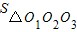 +3S弓
+3S弓∵△O1O2O3为正三角形,边长为r,
∴
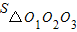 =
=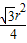 .
.∴S弓=
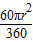 -
-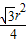 .
.S阴=
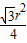 +3(
+3(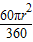 -
-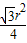 )=
)=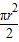
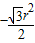 .
.(3)延长O2O1与⊙O1交于点A,⊙O1与⊙O4交于点B.
由(1)知,
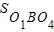 =
= (
(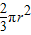 -
-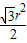 ).
).∵
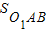 =
=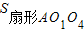 -
-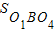 =
=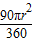 -
- (
(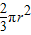 -
- )=
)=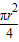
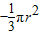 +
+ ,
,则
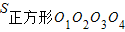 -4
-4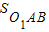 =r2-4(
=r2-4(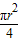
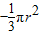 +
+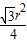 )=(
)=(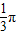 +1-
+1-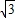 )r2.
)r2.点评:本题难度较大,考查圆与圆的位置关系中,互相交错的圆的图案的面积问题,同时考查了综合应用能力及推理能力.

练习册系列答案
相关题目