题目内容
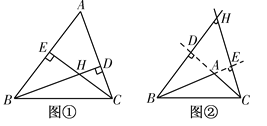
【题目】(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;并证明你的结论;
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,请你判断此时(1)中的等量关系是否仍然成立?并说明理由.
【答案】(1)∠BHC=180-∠A;(2)∠BHC=180-∠A.
【解析】试题分析:⑴由题易得∠ A+∠ ACE=90°,∠ ACE+∠DHC=90°,所以∠ A=∠ DHC,由图可知,∠ DHC与∠ BHC互补,故∠ A与∠ BHC互补.
⑵由⑴可知,∠BHC=∠ EAC,由图可知,∠ EAC与∠ BAC互补,所以∠ BHC与∠ BAC互补,故⑴中结论仍然成立.
试题解析:(1)∵BD⊥ AC , ∴ ∠ ADB=90°.
∵ CE⊥ AB , ∴∠ AEC=90°.
∵∠ A+∠ ADB+∠ AEC+∠ DHE=360°,
∴∠ DHE= 360°-(∠ A+∠ ADB+∠ AEC)=360°-(∠ A+90°+90°)=180°-∠ A,
∴ ∠ BHC=∠ DHE=180°-∠ A.
(2) ∵ BD⊥ AC ,∴ ∠ ADH=90°.
∵ CE⊥ AB , ∴ ∠ AEH=90°.
∵ ∠ DAE+∠ ADH+∠ AEH+∠ BHC=360°,
∴ ∠ BHC=360°-(∠ DAE+∠ ADH+∠ AEH)=360°-(∠ DAE+90°+90°)=180°-∠ DAE,
∴ ∠ BHC=180°-∠ A.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目