题目内容
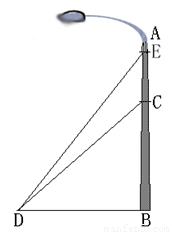
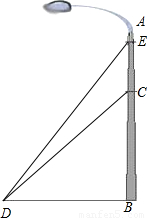
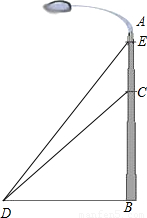
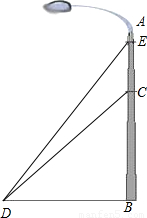
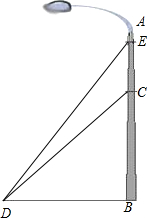如图，我市某广场一灯柱AB被一钢缆CD固定，CD与地面成40°夹角，且DB=5m，则BC的长度是多少？现再在C点上方2m处加固另一条钢缆ED，那么钢缆ED的长度为多少？（结果保留三个有效数字）
分析：要先求BE的长，就要求BC的长，而在Rt△CDB的中，已知一边和一个锐角，满足解直角三角形的条件，可求出BC的长，再由勾股定理求得ED的长．
解答：解：在Rt△BCD中，∵BD=5，
∵tan40°=
，
∴BC=5tan40°=4.1955≈4.20．
在Rt△BCD中，BE=BC+CE=6.20，
∴DE=
=
=
≈7.96
答：BC的长度约为4.20m，钢缆ED的长度约7.96m．
∵tan40°=
| BC |
| BD |
∴BC=5tan40°=4.1955≈4.20．
在Rt△BCD中，BE=BC+CE=6.20，
∴DE=
| BE2+DB2 |
=
| 38.44+25 |
| 63.44 |
≈7.96
答：BC的长度约为4.20m，钢缆ED的长度约7.96m．
点评：这两个直角三角形有公共的直角边，先利用公共边的解决此类题目的基本出发点．
练习册系列答案
相关题目
】
