题目内容
【题目】已知,如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,如果动点
运动,如果动点![]() 以1
以1![]() ,
,![]() 以2
以2![]() 的速度同时出发,设运动时间为
的速度同时出发,设运动时间为![]() ,解答下列问题:
,解答下列问题:
(1)当![]() __________
__________![]() 时,
时,![]() ;
;
(2)连接![]() .
.
①当![]() 时,求线段
时,求线段![]() 的长;
的长;
②在运动过程中,![]() 的形状不断发生变化,它能否构成直角三角形?如果能则求出此时
的形状不断发生变化,它能否构成直角三角形?如果能则求出此时![]() 的值,如果不能,请说明理由.
的值,如果不能,请说明理由.
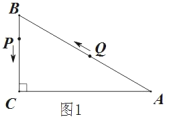
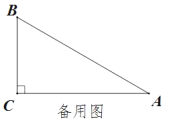
【答案】(1)6;(2)①![]() ,②能,当t为4.5或7.2时,△BPQ是直角三角形.
,②能,当t为4.5或7.2时,△BPQ是直角三角形.
【解析】
(1)先求得AB的长,再设BP=t,AQ=2t,则BQ=18-2t,即可求得t的值;
(2)①作QM⊥BC于M,QN⊥AC于N,在Rt△PQM中,利用勾股定理即可求解;
②分两种情况讨论当PQ⊥BC和PQ⊥BA,利用直角三角形的性质解答即可.
(1)在Rt△ABC中,∠C=90°,∠A=30°,BC=9 cm
∴AB=2 BC =18 cm,
由P、Q的运动速度可知:BP=t,AQ=2t,则BQ=18-2t,
根据题意:BP=BQ,即t=18-2t,
解得:t=6(s);
(2)在Rt△ABC中,∠C=90°,∠A=30°,BC=9 cm.
∴AB=18 cm,AC=![]() =
=![]() cm,
cm,
由P、Q的运动速度可知:BP=t,AQ=2t,
①当t=4时, BP=4,AQ=8,

作QM⊥BC于M,QN⊥AC于N,如答图1,
∵![]() ,
,
∴四边形CNQM为矩形,MC= QN,QM=CN,
∵∠A=30°,AQ=8,
∴QN=![]() ,
,![]() ,
,
∴PM=BC-BP-MC=9﹣4﹣4=1,
QM=CN=AC﹣AN=![]() ,
,
∴![]() (cm);
(cm);
②能构成直角三角形,有以下两种情况:
如答图2,当PQ⊥BC时,即PQ//AC,

∴∠BQP=∠A=30°,
∴BQ=2BP=2t,
即AB=BQ+AQ=2t +2t =4t=18,
解得:t=4.5(s);
如答图3,当PQ⊥BA时,
∵∠A=30°,
∴∠B=60°,
∴∠BPQ=30°,
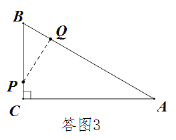
∴BP=2BQ=t,
∴BQ=0.5t,
即AB=AQ+BQ=2t+0.5t =2.5t=18,
解得:t=7.2(s);
综上所述,当t为4.5(s)或7.2(s)时,△BPQ是直角三角形.