题目内容
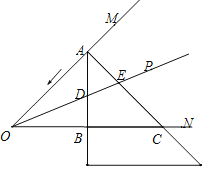
【题目】如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.
(1)点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.
(2)点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,猜想线段DF和AE有怎样的关系,并说明理由.
(3)若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,并证明你的猜想.
【答案】(1)、AD=AE,理由见解析;(2)、AE=DF,AE∥DF;理由见解析;(3)、OC=AC+AD,理由见解析.
【解析】
试题分析:(1)、根据AB⊥ON,AC⊥OM得出∠OAB=∠ACB,根据角平分线得出∠AOP=∠COP,从而得出∠ADE=∠AED,得出答案;(2)、根据点F与点A关于OP所在的直线对称得出AD=FD,AE=EF,然后证明△ADE和△FED全等,从而得出答案;(3)、延长EA到G点,使AG=AE,根据角度之间的关系得出CG=OC,根据(1)的结论得出AD=AE,根据AD=AE=AG得出答案.
试题解析:(1)、AD=AE
∵AB⊥ON,AC⊥OM. ∴∠OAB+∠BAC=90°,∠BAC+∠ACB=90°. ∴∠OAB=∠ACB.
∵OP平分∠MON, ∴∠AOP=∠COP. ∵∠ADE=∠AOP+∠OAB,∠AED=∠COP+∠ACB, ∴∠ADE=∠AED.
(2)、AE=DF,AE∥DF.
∵点F与点A关于OP所在的直线对称,∴AD=FD,AE=EF,
∵AD=AE,∴AD=FD=AE=EF,∵DE=DE, ∴△ADE≌△FED,∴∠AED=∠FDE,AE=DF,∴AE∥DF.
(3)、OC=AC+AD
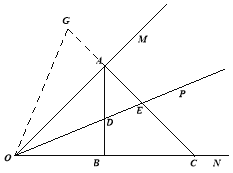
延长EA到G点,使AG=AE
∵∠OAE=90°∴OA⊥GE,∴OG=OE,∴∠AOG=∠EOA ∵∠AOC=45°,OP平分∠AOC ∴∠AOE=22.5°
∴∠AOG=22.5°,∠G=67.5° ∴∠COG=∠G=67.5° ∴CG=OC 由(1)得AD=AE
∵AD=AE=AG ∴AC+AD=OC

【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?