题目内容
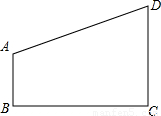
(2005•黄石)如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=4,BC=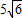 ,CD=9.
,CD=9.(1)在BC边上找一点O,过O点作OP⊥BC交AD于P,且OP2=AB•DC.求BO的长;
(2)以BC所在直线为x轴,OP所在直线为y轴,建立平面直角坐标系,求经过A、O、D三点的抛物线的解析式,并画出引抛物线的草图;
(3)在(2)中的抛物线上,连接AO、DO,证明:△AOD为直角三角形;过P点任作一直线与抛物线相交于A′(x1,y1),D′(x2,y2)两点,连接A′O、B′O,试问:△A′O′D′还为直角三角形吗?请说明理由.
【答案】分析:(1)本题可通过构建相似三角形来求解,先求出OP的长,然后过A作AF∥BC交CD于F,交OP于E,根据AB、OP、CD的长可求出DF、PE的长,然后根据△APE和△ADF相似可求出AE即BO的长.
(2)在(1)中求出了BO的长,即可得出OC的长,那么A、D的坐标就可求得.然后用待定系数法可求出抛物线的解析式.
(3)①证∠AOD=90°,可连接OA,OD通过证△AOB∽△ODC来得出∠AOB=∠ODC,进而求得∠AOB+∠DOC=∠ODC+∠DOC=90°,以此来证得∠AOD=90°.证两三角形相似时,可根据A、D的坐标求出AB,OB,OC,CD的长,然后证他们对应成比例即可.
②方法同①,可设直线的解析式为y=kx+b(k≠0),求出与抛物线的交点然后同①.
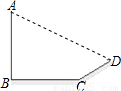
解答: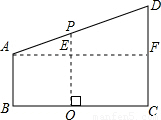 解:(1)在BC上取一点O,作OP⊥BC交AD于点P.
解:(1)在BC上取一点O,作OP⊥BC交AD于点P.
由OP2=BA•CD=4×9=36,得OP=6(取正),
过点A作直线AE∥BC,交OP于E,交CD于F.则BO=AE=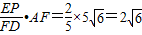 .(3分)
.(3分)
(2)根据题意建立直角坐标系,如图所示,则A(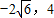 ),B(
),B(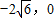 ),
),
O(0,0),C(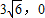 ),D(
),D(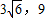 ),
),
过A、O、D三点的抛物线的解析式y=ax2+bx+c满足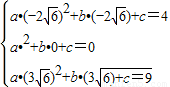
解得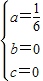 ,
,
∴抛物线的解析式为y= x2.
x2.
(3)连接OA、OD,在Rt△AOB和Rt△ODC中,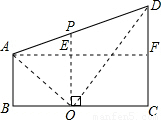
∴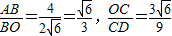 =
=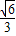
∴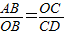 ,
,
∴Rt△AOB∽Rt△ODC,
∴∠AOD=180°-90°=90°,
∴△AOD为直角三角形.
点评:本题主要考查了直角梯形的性质、二次函数解析式的确定、相似三角形的判定和性质等知识点.
(2)在(1)中求出了BO的长,即可得出OC的长,那么A、D的坐标就可求得.然后用待定系数法可求出抛物线的解析式.
(3)①证∠AOD=90°,可连接OA,OD通过证△AOB∽△ODC来得出∠AOB=∠ODC,进而求得∠AOB+∠DOC=∠ODC+∠DOC=90°,以此来证得∠AOD=90°.证两三角形相似时,可根据A、D的坐标求出AB,OB,OC,CD的长,然后证他们对应成比例即可.
②方法同①,可设直线的解析式为y=kx+b(k≠0),求出与抛物线的交点然后同①.
解答:
 解:(1)在BC上取一点O,作OP⊥BC交AD于点P.
解:(1)在BC上取一点O,作OP⊥BC交AD于点P.由OP2=BA•CD=4×9=36,得OP=6(取正),
过点A作直线AE∥BC,交OP于E,交CD于F.则BO=AE=
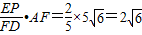 .(3分)
.(3分)(2)根据题意建立直角坐标系,如图所示,则A(
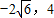 ),B(
),B(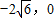 ),
),O(0,0),C(
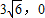 ),D(
),D(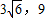 ),
),过A、O、D三点的抛物线的解析式y=ax2+bx+c满足
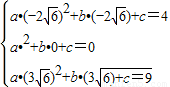
解得
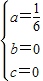 ,
,∴抛物线的解析式为y=
 x2.
x2.(3)连接OA、OD,在Rt△AOB和Rt△ODC中,

∴
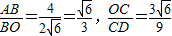 =
=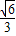
∴
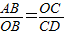 ,
,∴Rt△AOB∽Rt△ODC,
∴∠AOD=180°-90°=90°,
∴△AOD为直角三角形.
点评:本题主要考查了直角梯形的性质、二次函数解析式的确定、相似三角形的判定和性质等知识点.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 ,CD=9.
,CD=9.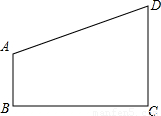
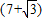 米
米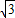 )米
)米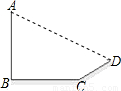
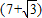 米
米 )米
)米