题目内容
(1)如图1,是某市公园周围街巷的示意图,A点表示1街与2巷的十字路口,B点表示3街与5巷的十字路口,如果用(1,2)→(2,2)→(3,2)→(3,3)→(3,4)→(3,5)表示由A点到B点的一条路径,那么,你能同样的方法写出由A点到B点尽可能近的其他两条路径吗?

(2)从正三角形、正四边形、正五边形、正六边形、正八边形、正十边形、正十二边形中任选两种正多边形镶嵌,请全部写出这两种正多边形.并从其中任选一种探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.
(3)如图2所示,已知AB∥CD,分别探索下列四个图形中∠P(均为小于平角的角)与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明.
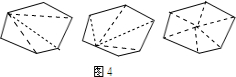
(4)阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.如图3给出了四边形的具体分割方法,分别将四边形分割成了2个、3个、4个小三角形.
请你按照上述方法将图4中的六边形进行分割,并写出得到的小三角形的个数以及求出每个图形中的六边形的内角和.试把这一结论推广至n边形,并推导出n边形内角和的计算公式.
解:(1)①(1,2)→(2,2)→(2,2)→(2,4)→(2,5)→(3,5);
②(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→(3,5);
(2)正三角形与正四边形;正三角形与正六边形;正三边形与正十二边形;正四边形与正八边形;正五边形与正十边形;
(3)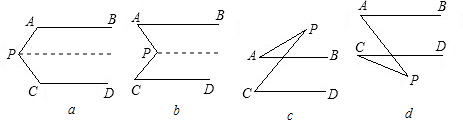
a、∠P+∠A+∠C=360°;b、∠P=∠A+∠C;c、∠P=∠C-∠A;d、∠P=∠A-∠C.
说明理由(以第三个为例):
已知AB∥CD,根据两直线平行,同位角相等及三角形的一个外角等于两不相邻内角之和,可得∠C=∠A+∠P.
提示:a、b均可过点P作AB的平行线PQ;c、d可通过外角来证.
(4)如图所示:
结合两个特殊图形,可以发现:
第一种分割法把n边形分割成了(n-2)个三角形,即内角和为(n-2)×180°;
第二种分割法把n边形分割成了(n-1)个三角形但多180°,即内角和为:(n-1)×180°-180°=(n-2)×180°;
第三种分割法把n边形分割成了n个三角形但多360°,即内角和为:n×180°-360°=(n-2)×180°.
分析:(1)根据已知的路线可以知道由A到B的一条路径只能向东,向北,所以根据这个方向即可确定其他的路径;
(2)分别求出各个正多边形的每个内角的度数,再利用镶嵌应符合一个内角度数能整除360即可作出判断;
(3)a,b都需要用到辅助线利用两直线平行,内错角相等的定理加以证明;c,d是利用两直线平行,同位角相等的定理和三角形外角的性质加以证明;
(4)图3中,第一个图形是作一个顶点出发的所有对角线对其进行分割;
第二个图形是连接多边形的其中一边上的一个点和各个顶点,对其进行分割;
第三个图形是连接多边形内部的任意一点和多边形的各个顶点,对其进行分割.
根据上述方法分别进行分割,可以发现所分割成的三角形的个数分别是4个,5个,6个.
根据这样的两个特殊图形,不难发现:
第一种分割法,分割成的三角形的个数比边数少2,
第二种分割法分割成的三角形的个数比边数少1,
第三种分割法分割成的三角形的个数等于多边形的边数.
点评:(1)题考查了坐标确定位置,是一个信息题目,根据题目隐含的信息找到题目中路径的规律,然后利用这个规律确定其他的路径.
(2)题考查了平面镶嵌(密铺),几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
(3)题考查了平行线的有关知识点,这是中考常考的题型;
(4)题考查了多边形内角与外角,此题要能够从特殊中发现规律,进而推广到一般.
②(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→(3,5);
(2)正三角形与正四边形;正三角形与正六边形;正三边形与正十二边形;正四边形与正八边形;正五边形与正十边形;
(3)
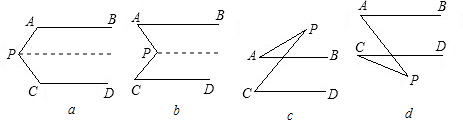
a、∠P+∠A+∠C=360°;b、∠P=∠A+∠C;c、∠P=∠C-∠A;d、∠P=∠A-∠C.
说明理由(以第三个为例):
已知AB∥CD,根据两直线平行,同位角相等及三角形的一个外角等于两不相邻内角之和,可得∠C=∠A+∠P.
提示:a、b均可过点P作AB的平行线PQ;c、d可通过外角来证.
(4)如图所示:

结合两个特殊图形,可以发现:
第一种分割法把n边形分割成了(n-2)个三角形,即内角和为(n-2)×180°;
第二种分割法把n边形分割成了(n-1)个三角形但多180°,即内角和为:(n-1)×180°-180°=(n-2)×180°;
第三种分割法把n边形分割成了n个三角形但多360°,即内角和为:n×180°-360°=(n-2)×180°.
分析:(1)根据已知的路线可以知道由A到B的一条路径只能向东,向北,所以根据这个方向即可确定其他的路径;
(2)分别求出各个正多边形的每个内角的度数,再利用镶嵌应符合一个内角度数能整除360即可作出判断;
(3)a,b都需要用到辅助线利用两直线平行,内错角相等的定理加以证明;c,d是利用两直线平行,同位角相等的定理和三角形外角的性质加以证明;
(4)图3中,第一个图形是作一个顶点出发的所有对角线对其进行分割;
第二个图形是连接多边形的其中一边上的一个点和各个顶点,对其进行分割;
第三个图形是连接多边形内部的任意一点和多边形的各个顶点,对其进行分割.
根据上述方法分别进行分割,可以发现所分割成的三角形的个数分别是4个,5个,6个.
根据这样的两个特殊图形,不难发现:
第一种分割法,分割成的三角形的个数比边数少2,
第二种分割法分割成的三角形的个数比边数少1,
第三种分割法分割成的三角形的个数等于多边形的边数.
点评:(1)题考查了坐标确定位置,是一个信息题目,根据题目隐含的信息找到题目中路径的规律,然后利用这个规律确定其他的路径.
(2)题考查了平面镶嵌(密铺),几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
(3)题考查了平行线的有关知识点,这是中考常考的题型;
(4)题考查了多边形内角与外角,此题要能够从特殊中发现规律,进而推广到一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
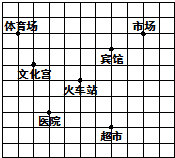 22、如图,这是某市部分简图,请建立适当的平面直角坐标系,分别写出各地的坐标.
22、如图,这是某市部分简图,请建立适当的平面直角坐标系,分别写出各地的坐标.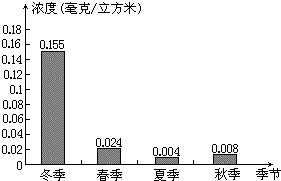 26、如图,这是某市环境监测中心监测统计的2003年该市市区空气中二氧化硫各季节日均值的统计图,空气中二氧化硫含量最高的季节与最低的季节的浓度之差等于
26、如图,这是某市环境监测中心监测统计的2003年该市市区空气中二氧化硫各季节日均值的统计图,空气中二氧化硫含量最高的季节与最低的季节的浓度之差等于 如图显示的是某市2006年至2008年财政总收入完成情况,图中数据精确到1亿元,由图中的数据可知2007年比2006年财政总收入增加了
如图显示的是某市2006年至2008年财政总收入完成情况,图中数据精确到1亿元,由图中的数据可知2007年比2006年财政总收入增加了 由.
由. 26、如图,AC是某市坏城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉路口分别是A、B、C经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2 km,∠DAC=15°.求∠ADB的大小及BD的长.
26、如图,AC是某市坏城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉路口分别是A、B、C经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2 km,∠DAC=15°.求∠ADB的大小及BD的长.