题目内容
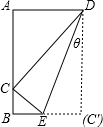如图：一张短边BC是10cm的长方形纸片，将按图所示的方法折叠，使得一顶点C恰好落在AB上，则折痕DE的长度（用θ表示）是分析：根据题意可知∠BEC=2θ，则cos∠BEC=
，设EC=x，则BE=10-x，继而可用θ表示出x，又DE=
，继而即可求出DE的长度．
| BE |
| CE |
| EC |
| sinθ |
解答：解：根据题意可知∠BEC=2θ，
设EC=x，则BE=10-x，
则cos∠BEC=cos2θ=
=
，
∴x=EC=
，
∴DE=
=
．
故答案为：
．
设EC=x，则BE=10-x，
则cos∠BEC=cos2θ=
| BE |
| CE |
| 10-x |
| x |
∴x=EC=
| 10 |
| 1+cos2θ |
∴DE=
| EC |
| sinθ |
| 10 |
| sinθ(1+cos2θ) |
故答案为：
| 10 |
| sinθ(1+cos2θ) |
点评：本题考查翻折变换的知识，难度适中，解题关键是先求出∠BEC的度数，然后用θ表示出EC的长．
练习册系列答案
相关题目
如图，把一张标准纸一次又一次对开，得到“2开”纸，“4开”纸，“8开”纸，“16开”纸…．已知标准纸的短边长为a．
如图：一张短边BC是10cm的长方形纸片，将按图所示的方法折叠，使得一顶点C恰好落在AB上，则折痕DE的长度（用θ表示）是________cm．