题目内容
已知a﹑b为正整数,a=b-2005,若关于x方程x2-ax+b=0有正整数解,则a的最小值是________.
95
分析:设两根为p,q,根据根与系数的关系,可知(p-1)(q-1)=pq-(p+q)+1=2006=2×59×17=1×2006=2×1003=17×118=34×59,因而求出a的最小整数值.
解答:设两根为p,q
p+q=a
pq=b=a+2005
(p-1)(q-1)=pq-(p+q)+1=2006=2×59×17
=1×2006=2×1003=17×118=34×59
所以a=p+q=(1+2006)+2=2009
或
a=p+q=(2+1003)+2=1007
或
a=17+118+2=137
或
a=34+59+2=95
所以最小值为95,
故答案为95.
点评:本题主要考查了一元二次方程根与系数的关系,有一点的难度.
分析:设两根为p,q,根据根与系数的关系,可知(p-1)(q-1)=pq-(p+q)+1=2006=2×59×17=1×2006=2×1003=17×118=34×59,因而求出a的最小整数值.
解答:设两根为p,q
p+q=a
pq=b=a+2005
(p-1)(q-1)=pq-(p+q)+1=2006=2×59×17
=1×2006=2×1003=17×118=34×59
所以a=p+q=(1+2006)+2=2009
或
a=p+q=(2+1003)+2=1007
或
a=17+118+2=137
或
a=34+59+2=95
所以最小值为95,
故答案为95.
点评:本题主要考查了一元二次方程根与系数的关系,有一点的难度.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
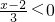 并且x为正整数,求
并且x为正整数,求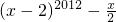 的值?
的值?