题目内容
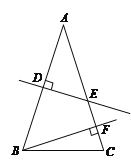
【题目】如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠ A的度数.
【答案】 36°
【解析】试题分析:连接BE,根据等腰三角形的性质得出∠ABC、∠C与∠A的关系,根据DE是线段AB的中垂线得出AE=BE,∠A=∠ABE,从而根据角平分线的性质得出∠A的度数.
试题解析:连接BE ∵△ABC是等腰三角形, ∴∠ABC=∠C=![]() ①,
①,
∵DE是线段AB的垂直平分线, ∴AE=BE, ∴∠A=∠ABE,
∵CE的垂直平分线正好经过点B,与AC相交于点可知△BCE是等腰三角形, ∴BF是∠EBC的平分线,
∴![]() (∠ABC﹣∠A)+∠C=90°,即
(∠ABC﹣∠A)+∠C=90°,即![]() (∠C﹣∠A)+∠C=90°②,
(∠C﹣∠A)+∠C=90°②,
①②联立得,∠A=36°. 故∠A=36°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目