题目内容
【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,D为BC上一点,AD=DC=2,
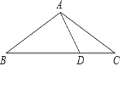
(1)求AC的长;
(2)求△ABC的面积.
【答案】(1)、2![]() ;(2)、3
;(2)、3![]() .
.
【解析】
试题分析:(1)、过点A作AE⊥BC,根据AB=AC,∠BAC=120°得出∠CAE=60°,∠C=30°,根据AD=DC=2,∠ADE=60°得出∠DAE=30°,DE=1,AE=![]() ,从而根据AC=2AE得出答案;(2)、根据S△ABC=
,从而根据AC=2AE得出答案;(2)、根据S△ABC=![]() BC×AE=
BC×AE=![]() ×2CE×AE=(ED+DC)×AE得出答案.
×2CE×AE=(ED+DC)×AE得出答案.
试题解析:(1)、过点A作AE⊥BC,如下图所示,
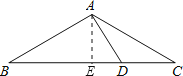
∵AB=AC,∠BAC=120°,∴∠CAE=60°,∠C=30°, ∵AD=DC=2,∴∠ADE=2∠C=60°,
∴∠DAE=30°,∴ED=![]() AD=1,AE=
AD=1,AE=![]() ∴AC=2AE=2
∴AC=2AE=2![]()
(2)、S△ABC=![]() BC×AE=
BC×AE=![]() ×2CE×AE=(ED+DC)×AE=3
×2CE×AE=(ED+DC)×AE=3![]()

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目