题目内容
正方形的四个顶点中有两个点的坐标为(0,0)、(2,2),那么,其他两个点的坐标为
(0,2)和(2,0)或(4,0)和(2,-2)或(0,4)和(-2,2)
(0,2)和(2,0)或(4,0)和(2,-2)或(0,4)和(-2,2)
.分析:由正方形的四个顶点中有两个点的坐标为(0,0)、(2,2),根据正方形的性质作图,即可求得答案.
解答: 解:如图:∵正方形的四个顶点中有两个点的坐标为(0,0)、(2,2),
解:如图:∵正方形的四个顶点中有两个点的坐标为(0,0)、(2,2),
∴①以OA为对角线作正方形,可得其他两个点的坐标为:(0,2)和(2,0);
②以OA为边作正方形,可得其他两个点的坐标为:(4,0)和(2,-2)或(0,4)和(-2,2).
∴其他两个点的坐标为:(0,2)和(2,0)或(4,0)和(2,-2)或(0,4)和(-2,2).
故答案为:(0,2)和(2,0)或(4,0)和(2,-2)或(0,4)和(-2,2).
 解:如图:∵正方形的四个顶点中有两个点的坐标为(0,0)、(2,2),
解:如图:∵正方形的四个顶点中有两个点的坐标为(0,0)、(2,2),∴①以OA为对角线作正方形,可得其他两个点的坐标为:(0,2)和(2,0);
②以OA为边作正方形,可得其他两个点的坐标为:(4,0)和(2,-2)或(0,4)和(-2,2).
∴其他两个点的坐标为:(0,2)和(2,0)或(4,0)和(2,-2)或(0,4)和(-2,2).
故答案为:(0,2)和(2,0)或(4,0)和(2,-2)或(0,4)和(-2,2).
点评:此题考查了正方形的性质.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
定义:在平面内,我们把既有大小又有方向的量叫做平面向量。平面向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向。其中大小相等,方向相同的向量叫做相等向量。
如以正方形![]() 的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同
的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同
的向量:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (由于
(由于![]() 和
和![]() 是相等向量,因此只算一个)。
是相等向量,因此只算一个)。
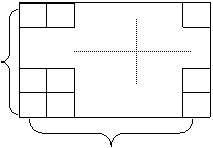
⑴ 作两个相邻的正方形(如图)。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
 |
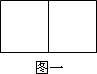
⑵ 作![]() 个相邻的正方形(如图)“
个相邻的正方形(如图)“![]() 一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
 …
…
共n个正方形
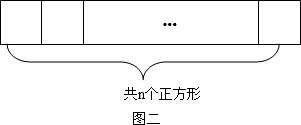
⑶ 作![]() 个相邻的正方形(如图)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为
个相邻的正方形(如图)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
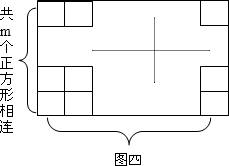
⑷ 作![]() 个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为
个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值。
的值。
| ||||
 | ||||
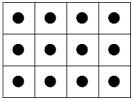 18、在3×4的方格网的每个小方格中心都放有一枚围棋子,至少要去掉( )枚围棋子,才能使得剩下的棋子中任意四枚都不够成正方形的四个顶点.
18、在3×4的方格网的每个小方格中心都放有一枚围棋子,至少要去掉( )枚围棋子,才能使得剩下的棋子中任意四枚都不够成正方形的四个顶点.