题目内容
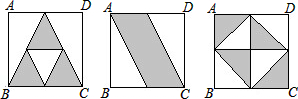 如图所示,图形中阴影部分的面积是正方形面积的
如图所示,图形中阴影部分的面积是正方形面积的分析:设正方形的边长为a,根据三角形的面积和平行四边形的面积分别表示出各图形中的阴影部分的面积,然后相除计算即可得解.
解答:解:设正方形的边长为a,
第一个图形中阴影部分的面积=
×(
a•a)=
a2,
第二个图形中阴影部分的面积=(
a)•a=
a2,
第三个图形中空白部分与阴影部分的面积相等,都是
a2,
所以,阴影部分的面积=
a2+
a2+
a2=
a2,
a2÷3a2=
,
所以,图形中阴影部分的面积是正方形面积的:
.
故答案为:
.
第一个图形中阴影部分的面积=
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
第二个图形中阴影部分的面积=(
| 1 |
| 2 |
| 1 |
| 2 |
第三个图形中空白部分与阴影部分的面积相等,都是
| 1 |
| 2 |
所以,阴影部分的面积=
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 8 |
| 11 |
| 8 |
| 11 |
| 24 |
所以,图形中阴影部分的面积是正方形面积的:
| 11 |
| 24 |
故答案为:
| 11 |
| 24 |
点评:本题考查了正方形的性质,主要利用了三角形的中位线定理,平行四边形的性质,仔细观察图形,得到各正方形中阴影部分的面积与正方形的关系是解题的关键,也是本题的难点.

练习册系列答案
相关题目
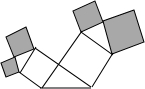 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的直角三角形斜边长为9cm,则四个阴影正方形的面积和是
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的直角三角形斜边长为9cm,则四个阴影正方形的面积和是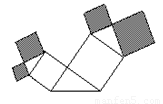
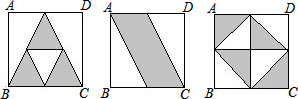 如图所示,图形中阴影部分的面积是正方形面积的________.
如图所示,图形中阴影部分的面积是正方形面积的________.