题目内容
【题目】已知命题:“P 是等边△ABC 内的一点,若 P 到三边的距离相等,则 PA=PB=PC.”
(1)写出它的逆命题.判断其逆命题成立吗?若成立,请给出证明.
(2)进一步证明:点 P 到等边△ABC 各边的距离之和为定值.
【答案】
(1)解:逆命题:P 是等边三角形 ABC内的一点,若PA=PB=PC,则P到三边的距离相等. 该逆命题成立.
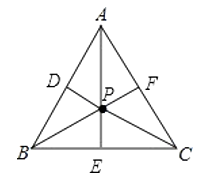
已知:如图:P是等边△ABC内的一点,若PA=PB=PC,PD⊥AB于D,PF⊥AC于F,PE⊥BC于E,
求证:PD=PE=PF.
证明:∵PA=PB,
∴P 在 AB 的垂直平分线上,
∵AC=BC,
∴C 在 AB 的垂直平分线上,
∴CP 是 AB 的垂直平分线,
∴CP 平分∠ACB,
同理,BP 平分∠ABC,AP 平分∠BAC,
∴P 是△ABC 三个角的角平分线的交点,
又∵PD⊥AB,PF⊥AC,PE⊥BC,
∴PD=PE=PF.
(2)证明:设AB边上的高为h,
∵AB=BC=AC 且 S△ABC=S△ABP +S△PBC +S△APC,
∴![]() AB.h=
AB.h=![]() AB.PD+
AB.PD+![]() BC.PE+
BC.PE+![]() AC.PF,
AC.PF,
∴h=PD+PE+PF,
∴点P到等边△ABC各边的距离之和为定值.定值为该三角形任意边上的高长.
【解析】(1)由垂直平分线的判定得出点P、点C均在 AB 的垂直平分线上,即CP 是 AB 的垂直平分线;再根据等腰三角形的性质得出CP 平分∠ACB;
同理,BP 平分∠ABC,AP 平分∠BAC,根据角平分线的性质得出PD=PE=PF.
(2)设AB边上的高为h,由 S△ABC=S△ABP +S△PBC +S△APC,从而得出h=PD+PE+PF,即为定值.
【考点精析】根据题目的已知条件,利用线段垂直平分线的判定和三角形的面积的相关知识可以得到问题的答案,需要掌握和一条线段两个端点距离相等的点,在这条线段的垂直平分线上;三角形的面积=1/2×底×高.

 阅读快车系列答案
阅读快车系列答案