Question

【题目】如图，AC是□ABCD的对角线，过对角线AC上一点M任作直线EF分别交DC于点E ， 交AB于点F ， 要使四边形AECF是平行四边形，则点M需满足的条件是 ．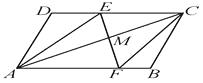

Answer 1

【答案】M为AC的中点
【解析】∵AC是□ABCD的对角线 ， M为AC的中点，
∴MA=MC ， ∠CAE=∠ACF ，
又∵∠AME=∠CMF ，
△AEM≌△CFM ，
∴ME=MF ，
又∵DE∥BC ， ，
∴四边形AECF是平行四边形．
故填M为AC的中点．
【考点精析】本题主要考查了平行四边形的判定的相关知识点，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形才能正确解答此题．