题目内容
若菱形的一个内角为60°,且边长为6cm,则较长的对角线的长为分析:因为菱形的四条边都相等,所以AB=AD,又因为∠BAD=60°,所以△ABD为等边三角形,所以BD=6cm.又因为AC⊥BD,OA=
AC,OD=
BD=3cm,所以可求得OA的长,即可求得AC的长.
| 1 |
| 2 |
| 1 |
| 2 |
解答: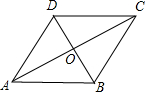 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,AD=AB=6cm,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=6cm,
∴OD=3cm,
∴OA=3
cm,
∴AC=6
cm.
∴较长的对角线的长为6
cm.
故答案为:6
.
 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,AD=AB=6cm,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=6cm,
∴OD=3cm,
∴OA=3
| 3 |
∴AC=6
| 3 |
∴较长的对角线的长为6
| 3 |
故答案为:6
| 3 |
点评:此题考查了菱形的性质:菱形的对角线互相平分且垂直,菱形的四条边都相等.

练习册系列答案
相关题目
若菱形的一个内角为60°,较短的一条对角线的长为6,则这个菱形的面积为( )
A、24
| ||
B、18
| ||
C、36
| ||
| D、36 |
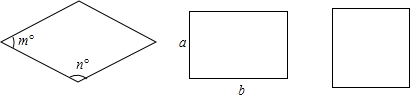
 15、如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.
15、如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.