题目内容
 如图,直线y=kx+b经过A(-1,1)和B(-
如图,直线y=kx+b经过A(-1,1)和B(-| 7 |
考点:一次函数与一元一次不等式
专题:待定系数法
分析:由于直线y=kx+b经过A(-1,1)和B(-
,0)两点,那么把A、B两点的坐标代入y=kx+b,用待定系数法求出k、b的值,然后解不等式组-x≥kx+b>0,即可求出解集.
| 7 |
解答:解:把A(-1,1)和B(-
,0)两点的坐标代入y=kx+b,
得
,
解得:
.
解不等式组:-x≥
x+
>0,
得:-
<x≤-1,
故答案为:-
<x≤-1.
| 7 |
得
|
解得:
|
解不等式组:-x≥
1-
| ||
| 6 |
7-
| ||
| 6 |
得:-
| 7 |
故答案为:-
| 7 |
点评:本题考查了用待定系数法求一次函数的解析式及一元一次不等式组的解法.本题中正确地求出k与b的值是解题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC.
如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC.
 随着车辆的增加,交通违规的现象越来越严重.为了解汽车速度的情况,交警抽取某雷达测速区某时段监测到的200辆汽车的时速(千米/时)进行整理,其中时速大于或等于30千米而小于40千米的汽车有10辆,…,得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重.为了解汽车速度的情况,交警抽取某雷达测速区某时段监测到的200辆汽车的时速(千米/时)进行整理,其中时速大于或等于30千米而小于40千米的汽车有10辆,…,得到其频数及频率如表: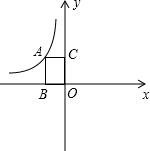 如图所示,设A为反比例函数y=
如图所示,设A为反比例函数y=