题目内容
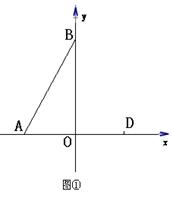
如图,点A在x轴负半轴上,点B在y轴正半轴上,线段AB长为6,将线段AB绕A点顺时针旋转60°,B点恰好落在x轴上点D处,点C在第一象限内且四边形ABCD是平行四边形.
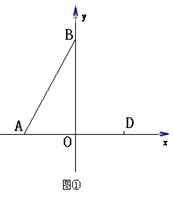
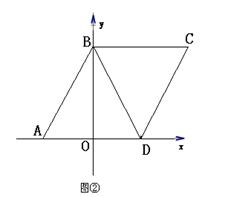
(1)求点C、点D的坐标;
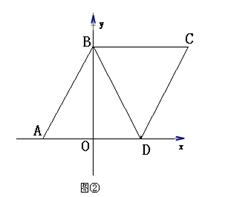
(2)如图②,若半径为1的⊙P从点A出发,沿A—B—D—C以每秒4个单位长的速度匀速移动,同时⊙P的半径以每秒1个单位长的速度匀速增加,当运动到点C时运动停止,运动时间为t秒,试问在整个运动过程中⊙P与y轴有公共点的时间共有几秒?
(3)在(2)的条件下,当⊙P在BD上运动时,过点C向⊙P作一条切线,t为何值时,切线长有最小值,最小值为多少?
(1)C(6,3 ),D(3,0);(2)
),D(3,0);(2) 或4或
或4或 ;(3)
;(3) ,
,
【解析】
试题分析:(1)先解Rt△ABO即可求得AO、BO的长,再根据旋转的性质即可求的结果;
(2)分0≤t≤1.5、1.5≤t≤3、3≤t≤4.5三种情况,根据直线与圆的位置关系求解即可;
(3)先根据题意表示出PH=|9?4t|,PQ=t+1,再根据勾股定理即可表示出QC关于t的函数关系式,再根据二次函数的性质求解即可.
(1)∵AB=6,∠BAO=60°
∴AO=3,BO=3 ,
,
∵点C在第一象限内且四边形ABCD是平行四边形
∴C(6,3 ),D(3,0) ;
),D(3,0) ;
(2)①t1= (0≤t≤1.5),
(0≤t≤1.5),
t2=4(1.5≤t≤3)舍去
t3=4(3≤t≤4.5)
t=t3-t1=4? =
=
(3)由题意可PH=|9?4t|,PQ=t+1
QC2 =PQ2+PC2 =(9-4t)
2+27- (t+1) 2=15t2-74t+107 =15(t? )2+
)2+
∵1.5≤t≤3
∴当t= 时,QC2 =
时,QC2 = ,QC=
,QC= .
.

考点:动点问题的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案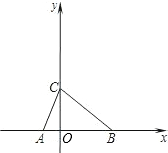 于x的一元二次方程x2-4mx+m2+2=0的两根,C(0,3),且S△ABC=6
于x的一元二次方程x2-4mx+m2+2=0的两根,C(0,3),且S△ABC=6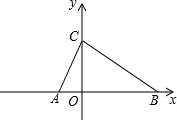 如图,点A在x轴负半轴上,点B、C分别在x轴、y轴的正半轴上且S△AOC:S△BOC=1:4,且OA、OB的长为关于x的方程x2-10x+m2=0的两个根.
如图,点A在x轴负半轴上,点B、C分别在x轴、y轴的正半轴上且S△AOC:S△BOC=1:4,且OA、OB的长为关于x的方程x2-10x+m2=0的两个根. S△ABC?若存在直接写出M的坐标,若不存在说明理由.
S△ABC?若存在直接写出M的坐标,若不存在说明理由.