题目内容
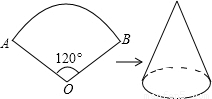
 如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,求:
如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,求:(1)围成的圆锥的侧面积.
(2)围成的圆锥的全面积.
分析:(1)利用扇形的面积公式即可求解;
(2)首先求得弧长即圆锥的底面半径,则底面的面积即可求解,底面积加上圆锥的侧面积即圆锥的全面积.
(2)首先求得弧长即圆锥的底面半径,则底面的面积即可求解,底面积加上圆锥的侧面积即圆锥的全面积.
解答:解:(1)圆锥的侧面积是:
=12π;
(2)扇形的弧长是:
=4π,则底面半径是2,
则底面面积是:4π,
则围成的圆锥的全面积是:12π+4π=16π.
| 120π×62 |
| 360 |
(2)扇形的弧长是:
| 120π×6 |
| 180 |
则底面面积是:4π,
则围成的圆锥的全面积是:12π+4π=16π.
点评:本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的底面半径为( )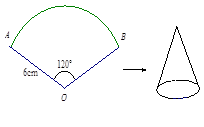
| A.2㎝ | B.4㎝ | C.1㎝ | D.8㎝ |
 (2013•襄城区模拟)如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的底面半径为( )
(2013•襄城区模拟)如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的底面半径为( )