题目内容
两圆的半径分别为a,b,圆心距为3.若|a+b-5|+a2-4a+4=0,则两圆的位置关系为
- A.内含
- B.相交
- C.外切
- D.外离
B
分析:先将|a+b-5|+a2-4a+4=0变形为|a+b-5|+(a-2)2=0,根据非负数的性质可求两圆的半径a,b的值,由两圆的半径和圆心距,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.
解答:|a+b-5|+a2-4a+4=0,
|a+b-5|+(a-2)2=0,
可得 ,
,
解得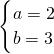 ,
,
则两圆的半径分别为2和3,圆心距为3,
∵2+3=5,3-3=1,1<3<5,
∴两圆的位置关系是相交.
故选B.
点评:此题考查了圆与圆的位置关系,非负数的性质.解题的关键是根据非负数的性质求出a,b的值,同时要掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.
分析:先将|a+b-5|+a2-4a+4=0变形为|a+b-5|+(a-2)2=0,根据非负数的性质可求两圆的半径a,b的值,由两圆的半径和圆心距,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.
解答:|a+b-5|+a2-4a+4=0,
|a+b-5|+(a-2)2=0,
可得
 ,
,解得
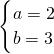 ,
,则两圆的半径分别为2和3,圆心距为3,
∵2+3=5,3-3=1,1<3<5,
∴两圆的位置关系是相交.
故选B.
点评:此题考查了圆与圆的位置关系,非负数的性质.解题的关键是根据非负数的性质求出a,b的值,同时要掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目