题目内容
先阅读下列的解答过程,然后作答:形如
m±2
|
| a |
| b |
| a |
| b |
| n |
m±2
|
(
|
| a |
| b |
7+4
|
解:首先把
7+4
|
7+2
|
由于4+3=7,4×3=12,即(
| 4 |
| 3 |
| 4 |
| 3 |
| 12 |
∴
7+4
|
7+2
|
(
|
| 3 |
由上述例题的方法化简:
(1)
13-2
|
(2)
7-
|
(3)
2-
|
分析:先把各题中的无理式变成
的形式,再根据范例分别求出各题中的a、b,即可求解.
m±2
|
解答:解:(1)
=
=
-
;
(2)
=
=
=
-
;
(3)
=
=
.
13-2
|
(
|
| 7 |
| 6 |
(2)
7-
|
7-2
|
(
|
| 5 |
| 2 |
(3)
2-
|
|
| ||||
| 2 |
点评:主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
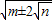 的化简,只要我们找到两个数a、b,使a+b=m,ab=n,使得
的化简,只要我们找到两个数a、b,使a+b=m,ab=n,使得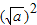 +
+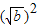 =m,
=m,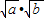 =
=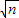 ,那么便有:
,那么便有: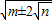 =
=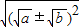 =
=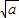 ±
±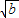 (a>b).
(a>b).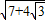 .
.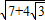 化为
化为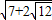 ,这里m=7,n=12,由于4+3=7,4×3=12
,这里m=7,n=12,由于4+3=7,4×3=12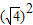 +
+ =7,
=7,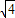 ×
×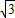 =
=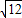
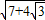 =
= =
=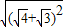 =2+
=2+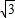 .
. .
.