题目内容
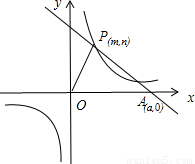
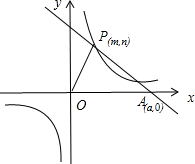 已知:O是坐标原点,P(m,n)(m>0)是函数y=
已知:O是坐标原点,P(m,n)(m>0)是函数y=| k |
| x |
| n4 |
| 4 |
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠
| n4 |
| 2 |
分析:(1)根据三角形的面积公式得到s=
a•n.而s=1+
,把n=1代入就可以得到a的值.
(2)易证△OPA是等腰直角三角形,得到m=n=
,根据三角形的面积S=
•an,就可以解得k的值.
(3)易证△OPQ∽△OAP,根据相似三角形面积的比等于相似比的平方,就可以得到关于k,n的方程,从而求出k,n的值.得到OP的值.
| 1 |
| 2 |
| n4 |
| 4 |
(2)易证△OPA是等腰直角三角形,得到m=n=
| a |
| 2 |
| 1 |
| 2 |
(3)易证△OPQ∽△OAP,根据相似三角形面积的比等于相似比的平方,就可以得到关于k,n的方程,从而求出k,n的值.得到OP的值.
解答:解:过点P作PQ⊥x轴于Q,则PQ=n,OQ=m,
(1)当n=1时,s=
,(1分)
∴a=
=
.(3分)
(2)解法一:∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.(4分)
∴m=n=
.(5分)
∴1+
=
•an.
即n4-4n2+4=0,(6分)
∴k2-4k+4=0,
∴k=2.(7分)
解法二:∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.(4分)
∴m=n.(5分)
设△OPQ的面积为s1
则:s1=
∴
•mn=
(1+
),
即:n4-4n2+4=0,(6分)
∴k2-4k+4=0,
∴k=2.(7分)
(3)解法一:∵PA⊥OP,PQ⊥OA,
∴△OPQ∽△OAP.
设:△OPQ的面积为s1,则
=
(8分)
即:
=
化简得:
2n4+2k2-kn4-4k=0(9分)
(k-2)(2k-n4)=0,
∴k=2或k=
(舍去),(10分)
∴当n是小于20的整数时,k=2.
∵OP2=n2+m2=n2+
又m>0,k=2,
∴n是大于0且小于20的整数.
当n=1时,OP2=5,
当n=2时,OP2=5,
当n=3时,OP2=32+
=9+
=
,(11分)
当n是大于3且小于20的整数时,
即当n=4、5、6…19时,OP2的值分别是:
42+
、52+
、62+
…192+
,
∵192+
>182+
>32+
>5,(12分)
∴OP2的最小值是5.(13分)
(1)当n=1时,s=
| 5 |
| 4 |
∴a=
| 2s |
| n |
| 5 |
| 2 |
(2)解法一:∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.(4分)
∴m=n=
| a |
| 2 |
∴1+
| n4 |
| 4 |
| 1 |
| 2 |
即n4-4n2+4=0,(6分)
∴k2-4k+4=0,
∴k=2.(7分)
解法二:∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.(4分)
∴m=n.(5分)
设△OPQ的面积为s1
则:s1=
| s |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n4 |
| 4 |
即:n4-4n2+4=0,(6分)
∴k2-4k+4=0,
∴k=2.(7分)
(3)解法一:∵PA⊥OP,PQ⊥OA,
∴△OPQ∽△OAP.
设:△OPQ的面积为s1,则
| s1 |
| s |
| PO2 |
| AO2 |
即:
| ||
1+
|
n2+
| ||||
|
2n4+2k2-kn4-4k=0(9分)
(k-2)(2k-n4)=0,
∴k=2或k=
| n4 |
| 2 |
∴当n是小于20的整数时,k=2.
∵OP2=n2+m2=n2+
| k2 |
| n2 |
∴n是大于0且小于20的整数.
当n=1时,OP2=5,
当n=2时,OP2=5,
当n=3时,OP2=32+
| 4 |
| 32 |
| 4 |
| 9 |
| 85 |
| 9 |
当n是大于3且小于20的整数时,
即当n=4、5、6…19时,OP2的值分别是:
42+
| 4 |
| 42 |
| 4 |
| 52 |
| 4 |
| 62 |
| 4 |
| 192 |
∵192+
| 4 |
| 192 |
| 4 |
| 182 |
| 4 |
| 32 |
∴OP2的最小值是5.(13分)
点评:本题是函数与三角形相结合的题目,题目的难度较大.

练习册系列答案
相关题目
 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+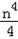 .(1)当n=1时,求点A的坐标;
.(1)当n=1时,求点A的坐标;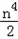 ,求OP2的最小值.
,求OP2的最小值.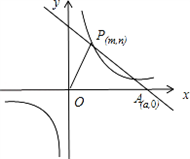
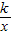 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+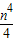 .
.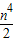 ,求OP2的最小值.
,求OP2的最小值.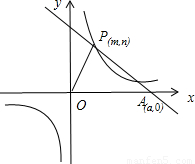
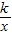 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+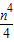 .
. ,求OP2的最小值.
,求OP2的最小值.
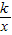 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+ .
.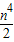 ,求OP2的最小值.
,求OP2的最小值.