题目内容
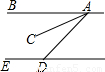
 如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是________.
如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是________.
134°
分析:根据平行线的性质(两直线平行,同旁内角互补)以及角平分线的性质可知:∠EDA=180°-2∠BAC.
解答:∵AC平分∠BAD,∠BAC=23°,
∴∠BAD=2∠BAC=46°;
又∵BA∥ED,
∴∠BAD+∠EDA=180°(两直线平行,同旁内角互补)
∴∠EDA=180°-46°=134°;
故答案是:134°.
点评:本题考查了平行线的性质以及角平分线的定义.解答该题时,利用两直线平行,同旁内角互补以及角平分线的性质找到∠EDA与已知角∠BAC的数量关系的.
分析:根据平行线的性质(两直线平行,同旁内角互补)以及角平分线的性质可知:∠EDA=180°-2∠BAC.
解答:∵AC平分∠BAD,∠BAC=23°,
∴∠BAD=2∠BAC=46°;
又∵BA∥ED,
∴∠BAD+∠EDA=180°(两直线平行,同旁内角互补)
∴∠EDA=180°-46°=134°;
故答案是:134°.
点评:本题考查了平行线的性质以及角平分线的定义.解答该题时,利用两直线平行,同旁内角互补以及角平分线的性质找到∠EDA与已知角∠BAC的数量关系的.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 (2012•铁岭)如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是
(2012•铁岭)如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是