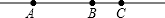题目内容
直线l上有三个不同的点A、B、C,且AB=BC.有以下说法:
①线段AB和线段BC关于某一定点成中心对称;
②线段AC是中心对称图形;
③线段AB是中心对称图形;
④直线l是中心对称图形.
其中正确的说法有( )
①线段AB和线段BC关于某一定点成中心对称;
②线段AC是中心对称图形;
③线段AB是中心对称图形;
④直线l是中心对称图形.
其中正确的说法有( )
分析:根据中心对称图形定义,我们可知图形绕交点旋转180°后,仍然能与原图形重合,所以两条直线的交点即为图形的对称中心,即可得出答案.
解答:解:①线段AB和线段BC关于某一定点成中心对称,正确;
②线段AC是中心对称图形,正确;
③线段AB是中心对称图形,正确;
④直线l是中心对称图形,正确.
其中正确的说法有4个;
故选A.
②线段AC是中心对称图形,正确;
③线段AB是中心对称图形,正确;
④直线l是中心对称图形,正确.
其中正确的说法有4个;
故选A.
点评:此题考查了中心对称,如果一个图形绕某一点旋转180°后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
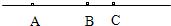
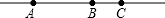 如图,直线上有三个不同的点A、B、C,且AB≠BC.那么,到A、B、C三点距离的和最小的点
如图,直线上有三个不同的点A、B、C,且AB≠BC.那么,到A、B、C三点距离的和最小的点