题目内容
两艘渔船同时从O点出发,甲船以40海里/小时的速度沿北偏东45°的方向航行,乙船沿正东方向航行,2小时后甲船到达小岛P处,发现乙船恰好位于甲船正南方向的H处,以O为坐标原点,建立如图所示的直角坐标系.
(1)P点的坐标是______,乙船的速度是______海里/小时(结果保留根号);
(2)若乙船发现正东方向有另一小岛M,且M位于P点南偏东60°的方向上,若乙船 速度不变,它再航行多长时间可以到达小岛M?(
速度不变,它再航行多长时间可以到达小岛M?( 取1.7,结果保留两个有效数字).
取1.7,结果保留两个有效数字).
解:(1)∵甲船以40海里/小时的速度沿北偏东45°的方向行驶2小时,
∴OP=40×2=80海里,PH=OH=40 海里,
海里,
故P点的坐标为(40 ,40
,40 ),
),
∴乙船的速度为: =20
=20 海里/小时.
海里/小时.
(2)在Rt△PHM中,PH=40 ,∠HPM=60°,
,∠HPM=60°,
∴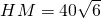 ,
,
∴t乙=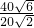 =2
=2 =3.4(小时).
=3.4(小时).
∴乙船再航行3.4小时可以到达小岛M.
分析:(1)求出PH和OH的长,即可得出点P的坐标,同时即可求出乙船的速度;
(2)先求出HM的值,由(1)中求出的乙船的速度,即可求出乙船的行驶时间.
点评:本题考查解直角三角形的应用中的方向角问题,难度适中,注意细心运算即可.
∴OP=40×2=80海里,PH=OH=40
 海里,
海里,故P点的坐标为(40
 ,40
,40 ),
),∴乙船的速度为:
 =20
=20 海里/小时.
海里/小时.(2)在Rt△PHM中,PH=40
 ,∠HPM=60°,
,∠HPM=60°,∴
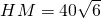 ,
,∴t乙=
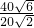 =2
=2 =3.4(小时).
=3.4(小时).∴乙船再航行3.4小时可以到达小岛M.
分析:(1)求出PH和OH的长,即可得出点P的坐标,同时即可求出乙船的速度;
(2)先求出HM的值,由(1)中求出的乙船的速度,即可求出乙船的行驶时间.
点评:本题考查解直角三角形的应用中的方向角问题,难度适中,注意细心运算即可.

练习册系列答案
相关题目
100年前,豪华游轮“泰坦尼克号”发生海难沉入大西洋.这是和平时期死伤人数最惨重的海难之一,也是最广为人知的海上事故之一.
结合所给材料回答问题:
(1)从一、二、三等舱乘客的幸存率,你能得出什么结论;从男人、女人、儿童、船员的幸存率,你能得出什么结论;写出一条不同于以上两条,你认为有意义的结论;
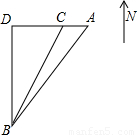
(2)假设B点是“泰坦尼克号”事故地点,在A点的三艘船只收到求救信号后立即前去营救:1号船从A点直线驶向B点;2号船先向西行驶到C点,再直线前往B点;3号先向西行驶100海里到B点正北方D点,再直线前往B点.搜救时海上刮正东风,三艘船顺风行驶速度都是24海里/时,非顺风速度都是12海里/时,若∠BAD=45°,∠BCD=60°,三艘船同时从A点出发,请说明谁先到达营救地点B.(参考数据: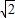 ≈1.4,
≈1.4,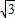 ≈1.7)
≈1.7)
| 成员 | 成员级别 | 乘员总人数 | 获救比率 | 死亡比率 | 获救人数 | 死亡人数 |
| 儿童 | 头等舱 | 6 | 85% | 17% | 5 | 1 |
| 二等舱 | 24 | 100% | 0% | 24 | ||
| 三等舱 | 79 | 34% | 66% | 27 | 52 | |
| 女子 | 头等舱 | 144 | 97% | 3% | 140 | 4 |
| 二等舱 | 93 | 86% | 14% | 80 | 13 | |
| 三等舱 | 165 | 46% | 54% | 76 | 89 | |
| 船员 | 23 | 87% | 13% | 20 | 3 | |
| 男子 | 头等舱 | 175 | 33% | 67% | 57 | 118 |
| 二等舱 | 168 | 8% | 92% | 14 | 154 | |
| 三等舱 | 462 | 16% | 84% | 75 | 387 | |
| 船员 | 885 | 22% | 78% | 192 | 693 |
(1)从一、二、三等舱乘客的幸存率,你能得出什么结论;从男人、女人、儿童、船员的幸存率,你能得出什么结论;写出一条不同于以上两条,你认为有意义的结论;
(2)假设B点是“泰坦尼克号”事故地点,在A点的三艘船只收到求救信号后立即前去营救:1号船从A点直线驶向B点;2号船先向西行驶到C点,再直线前往B点;3号先向西行驶100海里到B点正北方D点,再直线前往B点.搜救时海上刮正东风,三艘船顺风行驶速度都是24海里/时,非顺风速度都是12海里/时,若∠BAD=45°,∠BCD=60°,三艘船同时从A点出发,请说明谁先到达营救地点B.(参考数据:
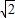 ≈1.4,
≈1.4,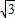 ≈1.7)
≈1.7)
 ,∠BCD=60°,三艘船同时从A点出发,请说明谁先到达营救地点B.(参考数据:
,∠BCD=60°,三艘船同时从A点出发,请说明谁先到达营救地点B.(参考数据: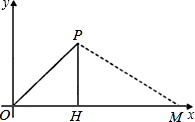 速度不变,它再航行多长时间可以到达小岛M?(
速度不变,它再航行多长时间可以到达小岛M?(