题目内容
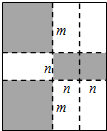
 用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是
用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是
- A.x+y=12
- B.x-y=2
- C.xy=35
- D.x2+y2=144
D
分析:能够根据大正方形和小正方形的面积分别求得正方形的边长,再根据其边长分别列方程,根据4个矩形的面积和等于两个正方形的面积的差列方程.
解答:A、根据大正方形的面积求得该正方形的边长是12,则x+y=12,正确;
B、根据小正方形的面积可以求得该正方形的边长是2,则x-y=2,正确;
C、根据4个矩形的面积和等于大正方形的面积减去小正方形的面积,即4xy=144-4=140,xy=35,正确;
D、错误.
故选D.
点评:此题关键是能够结合图形和图形的面积公式正确分析,运用排除法进行选择.
分析:能够根据大正方形和小正方形的面积分别求得正方形的边长,再根据其边长分别列方程,根据4个矩形的面积和等于两个正方形的面积的差列方程.
解答:A、根据大正方形的面积求得该正方形的边长是12,则x+y=12,正确;
B、根据小正方形的面积可以求得该正方形的边长是2,则x-y=2,正确;
C、根据4个矩形的面积和等于大正方形的面积减去小正方形的面积,即4xy=144-4=140,xy=35,正确;
D、错误.
故选D.
点评:此题关键是能够结合图形和图形的面积公式正确分析,运用排除法进行选择.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目

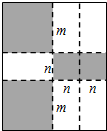 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.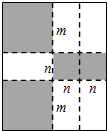 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.