题目内容
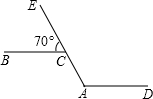如图：AD∥BC，点E在AC的延长线上，若∠BCE=70°，则∠CAD的度数是
- A.100°
- B.110°
- C.120°
- D.70°
B
分析：首先延长BC，由邻补角的定义，可得∠ECF的度数，又由AD∥BC，根据两直线平行，同位角相等，即可求得∠CAD的度数．
解答：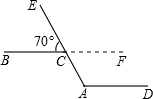
解：延长BC到F，
∵∠BCE=70°，
∴∠ECF=180°-∠BCE=110°，
∵AD∥BC，
∴∠CAD=∠ECF=110°．
故选B．
点评：此题考查了平行线的性质．注意两直线平行，同位角相等．
分析：首先延长BC，由邻补角的定义，可得∠ECF的度数，又由AD∥BC，根据两直线平行，同位角相等，即可求得∠CAD的度数．
解答：
解：延长BC到F，∵∠BCE=70°，
∴∠ECF=180°-∠BCE=110°，
∵AD∥BC，
∴∠CAD=∠ECF=110°．
故选B．
点评：此题考查了平行线的性质．注意两直线平行，同位角相等．
练习册系列答案
名师指导一卷通系列答案
相关题目
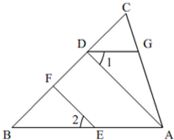25、如图，AD⊥BC于点D，∠1=2，∠CDG=∠B，请你判断EF与BC的位置关系，并加以证明，要求写出每步证明的理由．
11、如图，AD∥BC，点E在BD的延长线上，若∠ADE=155°，则∠DBC=
98、如图，AD∥BC，点E在的延长线上，CB=CE，试说明∠A=∠E．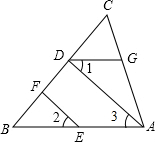
如图，AD⊥BC于点D，∠1=∠2，∠CDG=∠B，试说明EF⊥BC的理由．
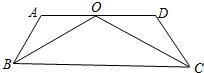如图，AD∥BC，点O在AD上，BO，CO分别平分∠ABC，∠DCB，若∠A+∠D=246°．