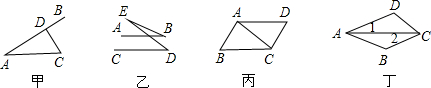
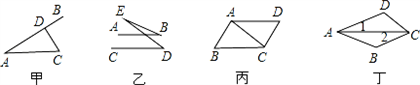
题目内容
如图,结合图形作出了如下判断或推理:
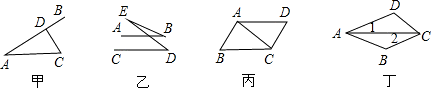
①如图甲,CD⊥AB,D为垂足,那么点C到AB的距离等于C、D两点间的距离;
②如图乙,如果AB∥CD,那么∠B=∠D;
③如图丙,如果∠ACD=∠CAB,那么AD∥BC;
④如图丁,如果∠1=∠2,∠D=120°,那么∠BCD=60°.
其中正确的个数是____个.
- A.1
- B.2
- C.3
- D.4
B
分析:根据点到直线的距离及两点间的距离的定义可判断①;
根据平行线的性质及三角形的外角的性质可判断②;
根据平行线的判定可判断③;
根据平行线的判定与性质可判断④.
解答: 解:①由于直线外一点到直线的垂线段的长度,叫做这点到这条直线的距离,故正确;
解:①由于直线外一点到直线的垂线段的长度,叫做这点到这条直线的距离,故正确;
②设AB与DE相交于点O.∵AB∥CD,∴∠AOE=∠D.又∵∠AOE>∠B,∴∠D>∠B,故错误;
③∵∠ACD=∠CAB,∴AB∥CD,故错误;
④∵∠1=∠2,∴AD∥BC,∴∠D+∠BCD=180°,又∵∠D=120°,∴∠BCD=60°,故正确.
故选B.
点评:本题主要考查了点到直线的距离的定义,平行线的判定与性质,三角形的外角的性质,属于基础知识,需牢固掌握.
分析:根据点到直线的距离及两点间的距离的定义可判断①;
根据平行线的性质及三角形的外角的性质可判断②;
根据平行线的判定可判断③;
根据平行线的判定与性质可判断④.
解答:
 解:①由于直线外一点到直线的垂线段的长度,叫做这点到这条直线的距离,故正确;
解:①由于直线外一点到直线的垂线段的长度,叫做这点到这条直线的距离,故正确;②设AB与DE相交于点O.∵AB∥CD,∴∠AOE=∠D.又∵∠AOE>∠B,∴∠D>∠B,故错误;
③∵∠ACD=∠CAB,∴AB∥CD,故错误;
④∵∠1=∠2,∴AD∥BC,∴∠D+∠BCD=180°,又∵∠D=120°,∴∠BCD=60°,故正确.
故选B.
点评:本题主要考查了点到直线的距离的定义,平行线的判定与性质,三角形的外角的性质,属于基础知识,需牢固掌握.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目