题目内容
等腰三角形腰长10cm,底边16cm,则面积为
- A.96cm2
- B.48cm2
- C.24cm2
- D.32cm2
B
分析:等腰三角形ABC,AB=AC,要求三角形的面积,可以先作出BC边上的高AD,则在Rt△ADB中,利用勾股定理就可以求出高AD,就可以求出三角形的面积.
解答: 解:作AD⊥BC于D,
解:作AD⊥BC于D,
∵AB=AC,
∴BD= BC=8cm,
BC=8cm,
∴AD=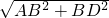 =6cm,
=6cm,
∴ =48cm2,
=48cm2,
故选B.
点评:本题主要运用了等腰三角形的性质:三线合一的性质,勾股定理.
分析:等腰三角形ABC,AB=AC,要求三角形的面积,可以先作出BC边上的高AD,则在Rt△ADB中,利用勾股定理就可以求出高AD,就可以求出三角形的面积.
解答:
 解:作AD⊥BC于D,
解:作AD⊥BC于D,∵AB=AC,
∴BD=
 BC=8cm,
BC=8cm,∴AD=
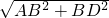 =6cm,
=6cm,∴
 =48cm2,
=48cm2,故选B.
点评:本题主要运用了等腰三角形的性质:三线合一的性质,勾股定理.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目