题目内容
校园内的一棵高大的树,如图所示,为了测量其高度,先坚一根木棒CD,通过测量影长来计算大树的高度AB,现已知CD=1m,DF=2.5m,BE=18m.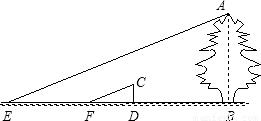
(1)求该大树的高度.
(2)在课外实践活动课上,老师准备了如下测量工具:(a)皮尺;(b)高为1米的测角器(c)长为1米的标杆.请你重新设计测量方案并回答下列问题:
①在你的设计方案中,选用的测量工具是(填工具的序号)______;
②在下图中画出你的测量方案示意图;

③你需要测量示意图中的哪些数据,请在图中用a,b,c,α,β等字母表示你测得的数据,并写出求树高AB的算式.
【答案】分析:(1)根据△ABE∽△CDF即可求出;
(2)结合(1)中求树高的方法,可知需要皮尺和标杆进行测量,其中需要测量的是树和标杆的影长.
解答:解:(1)由题意可知:△ABE∽△CDF,
∴ =
=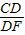 ,代入有
,代入有 ,
,
解得:AB=7.2m,
即该大树的高度为7.2m.
(2)①选用的测量工具是a和c.
②测量方案示意图如下所示:CD表示长为1m的标杆.

③需要测量的是DF和BE的长.
其中a=DF的长,b=BE的长.
点评:本题考查了解直角三角形的应用中的俯角仰角问题,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
(2)结合(1)中求树高的方法,可知需要皮尺和标杆进行测量,其中需要测量的是树和标杆的影长.
解答:解:(1)由题意可知:△ABE∽△CDF,
∴
 =
=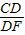 ,代入有
,代入有 ,
,解得:AB=7.2m,
即该大树的高度为7.2m.
(2)①选用的测量工具是a和c.
②测量方案示意图如下所示:CD表示长为1m的标杆.

③需要测量的是DF和BE的长.
其中a=DF的长,b=BE的长.
点评:本题考查了解直角三角形的应用中的俯角仰角问题,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目



