题目内容
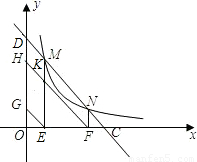
(2009•长宁区二模)如图,一次函数图象交反比例函数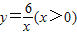 图象于点M、N(N在M右侧),分别交x轴、y轴于点C、D.过点M、N作ME、NF分别垂直x轴,垂足为E、F.再过点E、F作EG、FH平行MN直线,分别交y轴于点G、H,ME交FH于点K.
图象于点M、N(N在M右侧),分别交x轴、y轴于点C、D.过点M、N作ME、NF分别垂直x轴,垂足为E、F.再过点E、F作EG、FH平行MN直线,分别交y轴于点G、H,ME交FH于点K.(1)如果线段OE、OF的长是方程a2-4a+3=0的两个根,求该一次函数的解析式;
(2)设点M、N的横坐标分别为m、n,试探索四边形MNFK面积与四边形HKEG面积两者的数量关系;
(3)求证:MD=CN.
【答案】分析:(1)解方程a2-4a+3=0可以求出OE、OF,根据反比例函数解析式可以求出M,N的坐标,再利用待定系数法就求出了直线MN的解析式;
(2)容易知道DNFH、DMEG、DMKH为平行四边形,根据M、N在反比例函数的图象上,利用平行四边形的面积公式就可以求出它们的面积,从而确定两者的数量关系;
(3)此题既可以用几何方法,也可以用代数方法.几何方法设OE=m,OF=n,FC=a,然后用m、n表示ME、NF,然后利用△CNF∽△CME的对应边成比例可以得到a=m,再证明△EGO≌△CNF,就可以得到MD=CN.代数方法主要利用m,n表示直线MN,然后利用m,n表示D,C的坐标,最后用勾股定理求出DM,CN,就证明了题目的结论.
解答:解:(1)∵a2-4a+3=0,解得a1=1,a2=3,OE=1,OF=3
∴M(1,6),N(3,2)
∴直线MN解析式y=-2x+8;
(2)∵HF∥CD,NF∥ME,EG∥DM
∴四边形DNFH、DMEG、DMKH为平行四边形,
∴设SDMEG=ME•OE= =6(1分)
=6(1分)
SDNFH=NF•OF= =6(1分)
=6(1分)
∴SMNFK=SHKEG;(1分)
(3)①几何法:OE=m,OF=n,EF=n-m,ME= ,NF=
,NF= ,(1分)
,(1分)
设FC=a,
∵△CNF∽△CME,
∴ ,即
,即 ,得a=m(2分)
,得a=m(2分)
∵△EGO≌△CNF,EG=MD,得MD=CN(1分)
或②代数法:设直线MN为y=kx+b,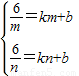 .得
.得 (1分)
(1分)
得D(0, )C(m+n,0)(1分)
)C(m+n,0)(1分)
DM= ,
,
CN= (1分)
(1分)
∴DM=CN.(1分)
点评:此题把一次函数,反比例函数等代数知识和平行四边形,全等三角形,相似三角形等几何知识结合在一起,综合性比较强,要求学生有较强的分析问题好解决问题的能力.
(2)容易知道DNFH、DMEG、DMKH为平行四边形,根据M、N在反比例函数的图象上,利用平行四边形的面积公式就可以求出它们的面积,从而确定两者的数量关系;
(3)此题既可以用几何方法,也可以用代数方法.几何方法设OE=m,OF=n,FC=a,然后用m、n表示ME、NF,然后利用△CNF∽△CME的对应边成比例可以得到a=m,再证明△EGO≌△CNF,就可以得到MD=CN.代数方法主要利用m,n表示直线MN,然后利用m,n表示D,C的坐标,最后用勾股定理求出DM,CN,就证明了题目的结论.
解答:解:(1)∵a2-4a+3=0,解得a1=1,a2=3,OE=1,OF=3
∴M(1,6),N(3,2)
∴直线MN解析式y=-2x+8;
(2)∵HF∥CD,NF∥ME,EG∥DM
∴四边形DNFH、DMEG、DMKH为平行四边形,
∴设SDMEG=ME•OE=
 =6(1分)
=6(1分)SDNFH=NF•OF=
 =6(1分)
=6(1分)∴SMNFK=SHKEG;(1分)
(3)①几何法:OE=m,OF=n,EF=n-m,ME=
 ,NF=
,NF= ,(1分)
,(1分)设FC=a,
∵△CNF∽△CME,
∴
 ,即
,即 ,得a=m(2分)
,得a=m(2分)∵△EGO≌△CNF,EG=MD,得MD=CN(1分)
或②代数法:设直线MN为y=kx+b,
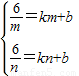 .得
.得 (1分)
(1分)得D(0,
 )C(m+n,0)(1分)
)C(m+n,0)(1分)DM=
 ,
,CN=
 (1分)
(1分)∴DM=CN.(1分)
点评:此题把一次函数,反比例函数等代数知识和平行四边形,全等三角形,相似三角形等几何知识结合在一起,综合性比较强,要求学生有较强的分析问题好解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

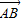 ,
,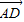 ,如用
,如用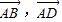 表示
表示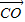 ,那么
,那么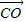 = .
= .