题目内容
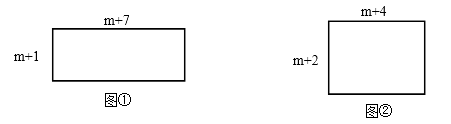
【题目】如图①，长方形的两边长分别为m+1，m+7；如图②，长方形的两边
长分别为m+2，m+4．(其中m为正整数)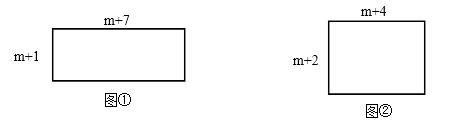
（1）图①中长方形的面积 
=
图②中长方形的面积 
=
比较： (填“＜”、“＝”或“＞”)
（2）现有一正方形，其周长与图①中的长方形周长相等，则
①求正方形的边长(用含m的代数式表示)；
②试探究：该正方形面积 
与图①中长方形面积 的差(即 - )是一个常数,求出这个常数．
（3）在(1)的条件下，若某个图形的面积介于 、 之间(不包括 、 )并且面积为整数，这样的整数值有且只有10个，求m的值．
【答案】
（1）m2+8m+7；m2+6m+8；>
（2）
解：①2（m+1+m+7）÷4=m+4；
②S-S1=（m+4）2-（m2+8m+7）=（m2+8m+16）-（m2+8m+7）=16-7=9.
（3）
解：由（1）S1-S2=2m-1，
当10<2m-1<11时，
<m≤6.
因为m为正整数，
所以m=6.
【解析】(1)S1=（m+1）（m+8）=m2+8m+7，
S2=（m+2）（m+4）=m2+6m+8，
S1-S2=m2+8m+7-（m2+6m+8）=2m-1,
因为m是正整数，最小为1，
所以S1-S2=2m-1≥1,
则S1>S2
练习册系列答案
阅读快车系列答案
相关题目
