题目内容
两艘轮船从同一港口同时出发,甲船时速40海里,乙船时速30海里,两个小时后,两船相距100海里,已知甲船的航向为北偏东46°,则乙船的航向为
- A.东偏南46°
- B.北偏西44°
- C.东偏南46°或西偏北46°
- D.无法确定
C
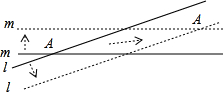
分析:根据题意画出图形,然后在直角三角形中利用勾股定理逆定理解答.
解答: 解:根据题意,OA=40×2=80海里,OB=30×2=60海里,
解:根据题意,OA=40×2=80海里,OB=30×2=60海里,
又因为AB=100海里,802+602=1002,
所以OB2+OA2=AB2,
根据勾股定理逆定理,
△AOB为直角三角形.
同理,△AOC为直角三角形.
所以∠AOB=90,
又因为∠1=46°,
所以∠2=180°-90°-46°=44°,
∠3=90°-44°=46°,
根据对顶角相等,∠4=∠3=46°,
则乙船的航向为东偏南46°或西偏北46°.
故选C.
点评:此题在作图时要注意有两种情况,不要漏解.
分析:根据题意画出图形,然后在直角三角形中利用勾股定理逆定理解答.
解答:
 解:根据题意,OA=40×2=80海里,OB=30×2=60海里,
解:根据题意,OA=40×2=80海里,OB=30×2=60海里,又因为AB=100海里,802+602=1002,
所以OB2+OA2=AB2,
根据勾股定理逆定理,
△AOB为直角三角形.
同理,△AOC为直角三角形.
所以∠AOB=90,
又因为∠1=46°,
所以∠2=180°-90°-46°=44°,
∠3=90°-44°=46°,
根据对顶角相等,∠4=∠3=46°,
则乙船的航向为东偏南46°或西偏北46°.
故选C.
点评:此题在作图时要注意有两种情况,不要漏解.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图所示的几何体是由五个小正方体搭建而成的.它的主视图是
如图所示的几何体是由五个小正方体搭建而成的.它的主视图是



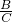 ÷D的正确运算顺序是
÷D的正确运算顺序是 是方程组
是方程组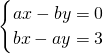 的解,则a、b的值是
的解,则a、b的值是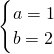
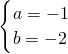
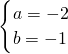
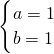
 如图,已知OB是⊙O的半径,点C、D在⊙O上,∠DCB=40°,则∠OBD=
如图,已知OB是⊙O的半径,点C、D在⊙O上,∠DCB=40°,则∠OBD=


