题目内容
(2006•吉林)如图,在平面直角坐标系xOy中,矩形OEFG的顶点E坐标为(4,0),顶点G坐标为(0,2).将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.(1)判断△OGA和△OMN是否相似,并说明理由;
(2)求过点A的反比例函数解析式;
(3)设(2)中的反比例函数图象交EF于点B,求直线AB的解析式;
(4)请探索:求出的反比例函数的图象,是否经过矩形OEFG的对称中心,并说明理由.

【答案】分析:(1)由已知,得∠OGA=∠M=90°,∠GOA=∠MON,易得△OGA∽△OMN.
(2)根据(1)的结论,可得AG的值,即A的坐标,设反比例函数y=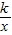 ,把A(1,2)代入,得k=2,即y=
,把A(1,2)代入,得k=2,即y=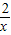 .
.
(3)易得B的坐标,设y=mx+n,把A(1,2),B(4, )代入可得方程组,解可得mn的值,代入可得直线AB的解析式;
)代入可得方程组,解可得mn的值,代入可得直线AB的解析式;
(4)设矩形OEFG的对称中心为Q,易得点Q坐标为(2,1),将其代入解析式,即可判断出答案.
解答:解:(1)△OGA∽△OMN.(1分)
由已知,得∠OGA=∠M=90°,∠GOA=∠MON,
∴△OGA∽△OMN.(2分)
(2)由(1)得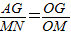 .
.
∴ ,AG=1,
,AG=1,
∴A(1,2).(3分)
设反比例函数y=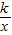 ,把A(1,2)代入,得k=2,即y=
,把A(1,2)代入,得k=2,即y=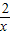 .(4分)
.(4分)
(3)∵点B的横坐标为4,把x=4代入y=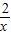 中得,y=
中得,y= ,即B(4,
,即B(4, ).(5分)
).(5分)
设y=mx+n,把A(1,2),B(4, )代入,得
)代入,得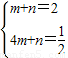 解得
解得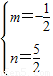
∴y=- x+
x+ .(8分)
.(8分)
(4)设矩形OEFG的对称中心为Q,则点Q坐标为(2,1).
把x=2代入y=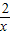 ,得y=1.
,得y=1.
∴反比例函数的图象经过矩形OEFG的对称中心.(10分)
点评:综合考查三角形相似的判定,反比例函数直线关系式的求法,及中心对称的有关知识.此题综合性强,有一定的难度,有利于培养同学们勇于探索的良好学习习惯.
(2)根据(1)的结论,可得AG的值,即A的坐标,设反比例函数y=
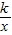 ,把A(1,2)代入,得k=2,即y=
,把A(1,2)代入,得k=2,即y=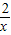 .
.(3)易得B的坐标,设y=mx+n,把A(1,2),B(4,
 )代入可得方程组,解可得mn的值,代入可得直线AB的解析式;
)代入可得方程组,解可得mn的值,代入可得直线AB的解析式;(4)设矩形OEFG的对称中心为Q,易得点Q坐标为(2,1),将其代入解析式,即可判断出答案.
解答:解:(1)△OGA∽△OMN.(1分)
由已知,得∠OGA=∠M=90°,∠GOA=∠MON,
∴△OGA∽△OMN.(2分)
(2)由(1)得
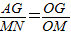 .
.∴
 ,AG=1,
,AG=1,∴A(1,2).(3分)
设反比例函数y=
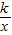 ,把A(1,2)代入,得k=2,即y=
,把A(1,2)代入,得k=2,即y=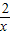 .(4分)
.(4分)(3)∵点B的横坐标为4,把x=4代入y=
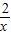 中得,y=
中得,y= ,即B(4,
,即B(4, ).(5分)
).(5分)设y=mx+n,把A(1,2),B(4,
 )代入,得
)代入,得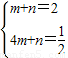 解得
解得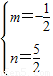
∴y=-
 x+
x+ .(8分)
.(8分)(4)设矩形OEFG的对称中心为Q,则点Q坐标为(2,1).
把x=2代入y=
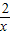 ,得y=1.
,得y=1.∴反比例函数的图象经过矩形OEFG的对称中心.(10分)
点评:综合考查三角形相似的判定,反比例函数直线关系式的求法,及中心对称的有关知识.此题综合性强,有一定的难度,有利于培养同学们勇于探索的良好学习习惯.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



