题目内容
【题目】如图,将一幅直角三角板叠放在一起,使直角顶点重合于点O. 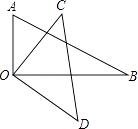
(1)若∠AOC=35°,求∠AOD的度数;
(2)问:∠AOC=∠BOD吗?说明理由;
(3)写出∠AOD与∠BOC所满足的数量关系,并说明理由.
【答案】
(1)解:∵∠COD=90°,∠AOC=35°,
∴∠AOD=∠AOC+∠COD=35°+90°=125°
(2)解:∠AOC=∠BOD,
理由是:∵∠AOB=∠COD=90°,
∴∠AOB﹣∠COB=∠COD﹣∠COB,
∴∠AOC=∠BOD
(3)解:∠AOD+∠BOC=180°,
理由是:∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC
=∠AOC+∠COD+∠BOC
=∠COD+∠AOB
=90°+90°
=180°
【解析】(1)把已知角的度数代入∠AOD=∠AOC+∠COD,求出即可;(2)已知∠AOB=∠COD=90°,都减去∠COB即可;(3)根据∠AOB=∠COD=90°即可求出答案.
【考点精析】通过灵活运用余角和补角的特征,掌握互余、互补是指两个角的数量关系,与两个角的位置无关即可以解答此题.

练习册系列答案
相关题目