题目内容
如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O是△EFG斜边上的中点.如图②,若整个△EFG从图①的位置出发,以1cm/s的速度沿射线AB方向平移,在△EFG平移的同时,点P从△EFG的顶点G出发,以1cm/s的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s),FG的延长线交AC于H,四边形OAHP的面积为y(cm2)(不考虑点P与G、F重合的情况).
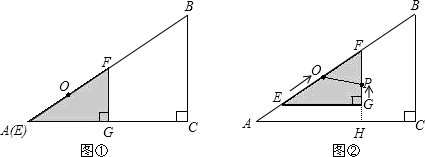
(1)当x为何值时,OP∥AC;
(2)求y与x之间的函数关系式,并确定自变量x的取值范围;
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13:24?若存在,求出x的值;若不存在,说明理由.(参考数据:1142=12996,1152=13225,1162=13456或4.42=19.36,4.52=20.25,4.62=21.16)
分析:(1)由于O是EF中点,因此当P为FG中点时,OP∥EG∥AC,据此可求出x的值.
(2)由于四边形AHPO形状不规则,可根据三角形AFH和三角形OPF的面积差来得出四边形AHPO的面积.三角形AHF中,AH的长可用AF的长和∠FAH的余弦值求出,同理可求出FH的表达式(也可用相似三角形来得出AH、FH的长).三角形OFP中,可过O作OD⊥FP于D,PF的长易知,而OD的长,可根据OF的长和∠FOD的余弦值得出.由此可求得y、x的函数关系式.
(3)先求出三角形ABC和四边形OAHP的面积,然后将其代入(2)的函数式中即可得出x的值.
(2)由于四边形AHPO形状不规则,可根据三角形AFH和三角形OPF的面积差来得出四边形AHPO的面积.三角形AHF中,AH的长可用AF的长和∠FAH的余弦值求出,同理可求出FH的表达式(也可用相似三角形来得出AH、FH的长).三角形OFP中,可过O作OD⊥FP于D,PF的长易知,而OD的长,可根据OF的长和∠FOD的余弦值得出.由此可求得y、x的函数关系式.
(3)先求出三角形ABC和四边形OAHP的面积,然后将其代入(2)的函数式中即可得出x的值.
解答:解:(1)∵Rt△EFG∽Rt△ABC
∴
=
,
=
∴FG=
=3cm
∵当P为FG的中点时,OP∥EG,EG∥AC
∴OP∥AC
∴x=
=
×3=1.5(s)
∴当x为1.5s时,OP∥AC.
(2)在Rt△EFG中,由勾股定理得EF=5cm
∵EG∥AH
∴△EFG∽△AFH
∴
=
=
∴AH=
(x+5),FH=
(x+5)
过点O作OD⊥FP,垂足为D
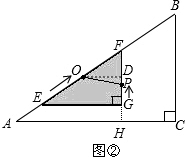
∵点O为EF中点
∴OD=
EG=2cm
∵FP=3-x
∴S四边形OAHP=S△AFH-S△OFP
=
•AH•FH-
•OD•FP
=
•
(x+5)•
(x+5)-
×2×(3-x)
=
x2+
x+3(0<x<3).
(3)假设存在某一时刻x,使得四边形OAHP面积与△ABC面积的比为13:24
则S四边形OAHP=
×S△ABC
∴
x2+
x+3=
×
×6×8
∴6x2+85x-250=0
解得x1=
,x2=-
(舍去)
∵0<x<3
∴当x=
(s)时,四边形OAHP面积与△ABC面积的比为13:24.
∴
| EG |
| AC |
| FG |
| BC |
| 4 |
| 8 |
| FG |
| 6 |
∴FG=
| 4×6 |
| 8 |
∵当P为FG的中点时,OP∥EG,EG∥AC
∴OP∥AC
∴x=
| ||
| 1 |
| 1 |
| 2 |
∴当x为1.5s时,OP∥AC.
(2)在Rt△EFG中,由勾股定理得EF=5cm
∵EG∥AH
∴△EFG∽△AFH
∴
| EG |
| AH |
| EF |
| AF |
| FG |
| FH |
∴AH=
| 4 |
| 5 |
| 3 |
| 5 |
过点O作OD⊥FP,垂足为D

∵点O为EF中点
∴OD=
| 1 |
| 2 |
∵FP=3-x
∴S四边形OAHP=S△AFH-S△OFP
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
=
| 6 |
| 25 |
| 17 |
| 5 |
(3)假设存在某一时刻x,使得四边形OAHP面积与△ABC面积的比为13:24
则S四边形OAHP=
| 13 |
| 24 |
∴
| 6 |
| 25 |
| 17 |
| 5 |
| 13 |
| 24 |
| 1 |
| 2 |
∴6x2+85x-250=0
解得x1=
| 5 |
| 2 |
| 50 |
| 3 |
∵0<x<3
∴当x=
| 5 |
| 2 |
点评:本题是比较常规的动态几何压轴题,第1小题运用相似形的知识容易解决,第2小题同样是用相似三角形建立起函数解析式,要说的是本题中说明了要写出自变量x的取值范围,而很多试题往往不写,要记住自变量x的取值范围是函数解析式不可分离的一部分,无论命题者是否交待了都必须写,第3小题只要根据函数解析式列个方程就能解决.

练习册系列答案
相关题目