题目内容
(2012•青岛)已知:如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(s)(0<t<4).解答下列问题:
(1)当t为何值时,PQ⊥AB?
(2)当点Q在BE之间运动时,设五边形PQBCD的面积为y(cm2),求y与t之间的函数关系式;
(3)在(2)的情况下,是否存在某一时刻t,使PQ分四边形BCDE两部分的面积之比为S△PQE:S五边形PQBCD=1:29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.
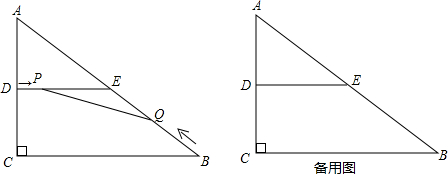
(1)当t为何值时,PQ⊥AB?
(2)当点Q在BE之间运动时,设五边形PQBCD的面积为y(cm2),求y与t之间的函数关系式;
(3)在(2)的情况下,是否存在某一时刻t,使PQ分四边形BCDE两部分的面积之比为S△PQE:S五边形PQBCD=1:29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.

分析:(1)如图①所示,当PQ⊥AB时,△PQE是直角三角形.解决问题的要点是将△PQE的三边长PE、QE、PQ用时间t表示,这需要利用相似三角形(△PQE∽△ACB)比例线段关系(或三角函数);
(2)本问关键是利用等式“五边形PQBCD的面积=四边形DCBE的面积-△PQE的面积”,如图②所示.为求△PQE的面积,需要求出QE边上的高,因此过P点作QE边上的高,利用相似关系(△PME∽△ABC)求出高的表达式,从而问题解决;
(3)本问要点是根据题意,列出一元二次方程并求解.假设存在时刻t,使S△PQE:S五边形PQBCD=1:29,则此时S△PQE=
S梯形DCBE,由此可列出一元二次方程,解方程即求得时刻t;点E到PQ的距离h利用△PQE的面积公式得到.
(2)本问关键是利用等式“五边形PQBCD的面积=四边形DCBE的面积-△PQE的面积”,如图②所示.为求△PQE的面积,需要求出QE边上的高,因此过P点作QE边上的高,利用相似关系(△PME∽△ABC)求出高的表达式,从而问题解决;
(3)本问要点是根据题意,列出一元二次方程并求解.假设存在时刻t,使S△PQE:S五边形PQBCD=1:29,则此时S△PQE=
| 1 |
| 30 |
解答: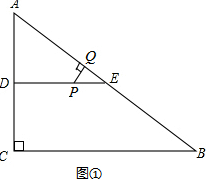 解:(1)如图①,在Rt△ABC中,
解:(1)如图①,在Rt△ABC中,
AC=6,BC=8
∴AB=
=10.
∵D、E分别是AC、AB的中点.
AD=DC=3,AE=EB=5,DE∥BC且
DE=
BC=4
∵PQ⊥AB,
∴∠PQB=∠C=90°
又∵DE∥BC
∴∠AED=∠B
∴△PQE∽△ACB
=
由题意得:PE=4-t,QE=2t-5,
即
=
,
解得t=
;
(2)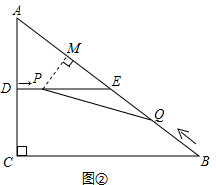 如图②,过点P作PM⊥AB于M,
如图②,过点P作PM⊥AB于M,
由△PME∽△ACB,得
=
,
∴
=
,得PM=
(4-t).
S△PQE=
EQ•PM=
(5-2t)•
(4-t)=
t2-
t+6,
S梯形DCBE=
×(4+8)×3=18,
∴y=18-(
t2-
t+6)=-
t2+
t+12.
(3)假设存在时刻t,使S△PQE:S五边形PQBCD=1:29,
则此时S△PQE=
S梯形DCBE,
∴
t2-
t+6=
×18,
即2t2-13t+18=0,
解得t1=2,t2=
(舍去).
当t=2时,
PM=
×(4-2)=
,ME=
×(4-2)=
,
EQ=5-2×2=1,MQ=ME+EQ=
+1=
,
∴PQ=
=
=
.
∵
PQ•h=
,
∴h=
•
=
(或
).
 解:(1)如图①,在Rt△ABC中,
解:(1)如图①,在Rt△ABC中,AC=6,BC=8
∴AB=
| 62+82 |
∵D、E分别是AC、AB的中点.
AD=DC=3,AE=EB=5,DE∥BC且
DE=
| 1 |
| 2 |
∵PQ⊥AB,
∴∠PQB=∠C=90°
又∵DE∥BC
∴∠AED=∠B
∴△PQE∽△ACB
| PE |
| AB |
| QE |
| BC |
由题意得:PE=4-t,QE=2t-5,
即
| 4-t |
| 10 |
| 2t-5 |
| 8 |
解得t=
| 41 |
| 14 |
(2)
 如图②,过点P作PM⊥AB于M,
如图②,过点P作PM⊥AB于M,由△PME∽△ACB,得
| PM |
| AC |
| PE |
| AB |
∴
| PM |
| 6 |
| 4-t |
| 10 |
| 3 |
| 5 |
S△PQE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
| 39 |
| 10 |
S梯形DCBE=
| 1 |
| 2 |
∴y=18-(
| 3 |
| 5 |
| 39 |
| 10 |
| 3 |
| 5 |
| 39 |
| 10 |
(3)假设存在时刻t,使S△PQE:S五边形PQBCD=1:29,
则此时S△PQE=
| 1 |
| 30 |
∴
| 3 |
| 5 |
| 39 |
| 10 |
| 1 |
| 30 |
即2t2-13t+18=0,
解得t1=2,t2=
| 9 |
| 2 |
当t=2时,
PM=
| 3 |
| 5 |
| 6 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |
EQ=5-2×2=1,MQ=ME+EQ=
| 8 |
| 5 |
| 13 |
| 5 |
∴PQ=
| PM2+MQ2 |
(
|
| ||
| 5 |
∵
| 1 |
| 2 |
| 3 |
| 5 |
∴h=
| 6 |
| 5 |
| 5 | ||
|
6
| ||
| 205 |
| 6 | ||
|
点评:本题是动点型综合题,解题关键是掌握动点运动过程中的图形形状、图形面积的表示方法.所考查的知识点涉及到勾股定理、相似三角形的判定与性质、三角形中位线定理、解方程(包括一元一次方程和一元二次方程)等,有一定的难度.注意题中求时刻t的方法:最终都是转化为一元一次方程或一元二次方程求解.

练习册系列答案
相关题目
 (2012•青岛)已知:线段a,c,∠α.
(2012•青岛)已知:线段a,c,∠α.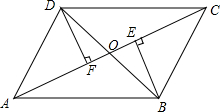 (2012•青岛)已知:如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
(2012•青岛)已知:如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.