题目内容
已知:如图,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A、B.(1)若点O到直线AB的距离为
| 12 |
| 5 |
| 3 |
| 4 |
(2)若点O到直线AB的距离为
| 12 |
| 5 |
| 1 |
| CD |
| 1 |
| BE |
(3)如图,若⊙O1经过点M(2,2),设△BOA的内切圆的直径为
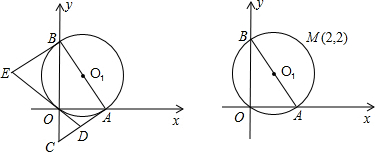 d,试判断d+AB的值是否会发生变化,若不变,求出其值;若变化,求其变化的范围.
d,试判断d+AB的值是否会发生变化,若不变,求出其值;若变化,求其变化的范围.
分析:(1)已知点O到直线AB的距离为
,且tan∠B=
,从O点作AB的垂线,利用三角函数关系求出OA、OB和OB的关系,利用△AOB的面积公式可求出AB的长度;
(2)延长BE交x轴于点F,过点O作OG⊥AB于点G,∵DO=DA,∴∠DOA=∠DAO,∴∠COD=∠DCO,DO=DA=DC,同理可证:EB=EO=EF,根据平行线段成比例的原理,可以求出结果.
| 12 |
| 5 |
| 3 |
| 4 |
(2)延长BE交x轴于点F,过点O作OG⊥AB于点G,∵DO=DA,∴∠DOA=∠DAO,∴∠COD=∠DCO,DO=DA=DC,同理可证:EB=EO=EF,根据平行线段成比例的原理,可以求出结果.
解答:解:(1)作OG⊥AB,垂足为点G,
∵tan∠B=
,设OA=3k,OB=4k,
∴AB=5k,(1分)
∵OA•OB=AB•OG=2S△AOB,即3k×4k=5k×
,∴k=1,(3分)
∴AB=5;(4分)
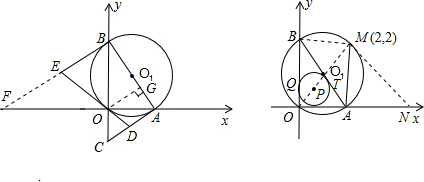
(2)延长BE交x轴于点F,过点O作OG⊥AB于点G,
∵DO=DA,
∴∠DOA=∠DAO,
∴∠COD=∠DCO,DO=DA=DC,同理可证:EB=EO=EF,(5分)
又∵AC∥OG∥BF,
∴
=
=
,∴
=
=
,
+
=
=1,
即
+
=
,(8分)
而OG=
=
,∴
+
=
;(9分)
(3)d+AB的值不会发生变化.
设△AOB的内切圆分别切OA、OB、AB于点P、Q、T,则d+AB=OQ+OP+QB+PA=OA+OB,
在x轴上取一点N,使AN=OB,连接OM、BM、AM、MN,
∵OM平分∠AOB,
∴∠BOM=∠MON=45°,AM=BM;
又∵∠MAN=∠OBM,OB=AN,
∴△BOM≌△ANM,(12分)
∴∠BOM=∠N=45°,
∴∠OMN=90°,
∴OA+OB=ON=
=
OM=4,
∴d+AB的值不会发生变化,其值为4.(14分)
∵tan∠B=
| 3 |
| 4 |
∴AB=5k,(1分)
∵OA•OB=AB•OG=2S△AOB,即3k×4k=5k×
| 12 |
| 5 |
∴AB=5;(4分)
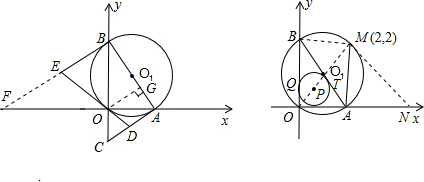
(2)延长BE交x轴于点F,过点O作OG⊥AB于点G,
∵DO=DA,
∴∠DOA=∠DAO,
∴∠COD=∠DCO,DO=DA=DC,同理可证:EB=EO=EF,(5分)
又∵AC∥OG∥BF,
∴
| OG |
| 2CD |
| OG |
| AC |
| BG |
| BA |
| OG |
| 2BE |
| OG |
| BF |
| AG |
| AB |
| OG |
| 2CD |
| OG |
| 2BE |
| BG+AG |
| AB |
即
| 1 |
| CD |
| 1 |
| BE |
| 2 |
| OG |
而OG=
| OA×OB |
| AB |
| 12 |
| 5 |
| 1 |
| CD |
| 1 |
| BE |
| 5 |
| 6 |
(3)d+AB的值不会发生变化.
设△AOB的内切圆分别切OA、OB、AB于点P、Q、T,则d+AB=OQ+OP+QB+PA=OA+OB,
在x轴上取一点N,使AN=OB,连接OM、BM、AM、MN,
∵OM平分∠AOB,
∴∠BOM=∠MON=45°,AM=BM;
又∵∠MAN=∠OBM,OB=AN,
∴△BOM≌△ANM,(12分)
∴∠BOM=∠N=45°,
∴∠OMN=90°,
∴OA+OB=ON=
| OM2+MN2 |
| 2 |
∴d+AB的值不会发生变化,其值为4.(14分)
点评:解题的关键要熟练掌握坐标的有关知识,利用图形结合来解决.

练习册系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.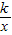 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
