题目内容
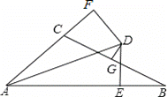
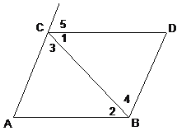
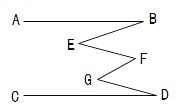
【题目】如图,AB∥CD.证明:∠B+∠F+∠D=∠E+∠G.
【答案】见解析
【解析】
作EM∥AB,FN∥AB,GK∥AB,可得AB∥ME∥FN∥GK∥CD,∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,∠B+∠3+∠4+∠D=∠1+∠2+∠5+∠6,由图可得
∠E+ ∠G=∠1+∠2+∠5+∠6,可得结论.
证明:作EM∥AB,FN∥AB,GK∥AB,

∵AB∥CD,
∴AB∥ME∥FN∥GK∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,
∴∠B+∠3+∠4+∠D=∠1+∠2+∠5+∠6,
又∵∠E+ ∠G=∠1+∠2+∠5+∠6,
∠B+ ∠F+ ∠D=∠B+ ∠3+∠4+ ∠D,
∴∠B+ ∠F+ ∠D=∠E+ ∠G.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
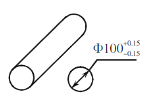
【题目】对某厂生产的一批轴进行检验,检验结果中轴的直径的各组频数、频率如表(每组含前一个边界值,不含后一个边界值),且轴直径的合格标准为![]() (单位:mm),有下列结论:①这批被检验的轴总数为50根;②a+b=0.44且x=y;③这批轴中没有直径恰为100.15mm的轴;④这一批轴的合格率是82%,若该厂生产1000根这样的轴,则其中恰好有180根不合格. 其中正确的有______个.
(单位:mm),有下列结论:①这批被检验的轴总数为50根;②a+b=0.44且x=y;③这批轴中没有直径恰为100.15mm的轴;④这一批轴的合格率是82%,若该厂生产1000根这样的轴,则其中恰好有180根不合格. 其中正确的有______个.
组别(mm) | 频数 | 频率 |
99.55~99.70 | x | a |
99.70~99.85 | 5 | 0.1 |
99.85~100.00 | 21 | 0.42 |
100.00~100.15 | 20 | b |
100.15~100.30 | 0 | 0 |
100.30~100.45 | y | 0.04 |