题目内容
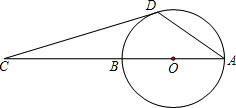 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D.若∠C=28°,则∠CDA=________度.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D.若∠C=28°,则∠CDA=________度.
121
分析:连接OD,把要求的∠CDA分成了两个角∠ODC与∠ODA,根据已知的CD与⊙O相切于点D,利用切线的性质可求出∠ODC等于90°,再根据已知的∠C的度数,利用三角形的内角和定理可得到∠DOC的度数,又根据圆的两半径相等得到OA=OD,根据等角对等边得到∠OAD=∠ODA,利用外角的性质可得到这两个角的和等于∠DOC,进而求出∠ODA的度数,最后用求出的∠ODC与∠ODA的和即可得到∠CDA的度数.
解答: 解:连接OD.
解:连接OD.
∵CD与⊙O相切于点D,
∴∠ODC=90°,又∠C=28°,
∴∠DOC=62°,
又∵OA=OD,
∴∠OAD=∠ODA,
又因为∠DOC是△AOD的外角,
∴∠DOC=∠OAD+∠ODA=62°,
∴∠OAD=∠ODA=31°,
∴∠CDA=∠ODC+∠ODA=90°+31°=121°.
故答案为:121.
点评:本题考查了圆的切线性质,等腰三角形的性质,三角形的内角和定理及外角性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.该题属于几何综合题,在解题时应注意把代数与几何图形的性质及计算与证明有机融合起来,进行分析、推理,从而达到解决问题的目的.
分析:连接OD,把要求的∠CDA分成了两个角∠ODC与∠ODA,根据已知的CD与⊙O相切于点D,利用切线的性质可求出∠ODC等于90°,再根据已知的∠C的度数,利用三角形的内角和定理可得到∠DOC的度数,又根据圆的两半径相等得到OA=OD,根据等角对等边得到∠OAD=∠ODA,利用外角的性质可得到这两个角的和等于∠DOC,进而求出∠ODA的度数,最后用求出的∠ODC与∠ODA的和即可得到∠CDA的度数.
解答:
 解:连接OD.
解:连接OD.∵CD与⊙O相切于点D,
∴∠ODC=90°,又∠C=28°,
∴∠DOC=62°,
又∵OA=OD,
∴∠OAD=∠ODA,
又因为∠DOC是△AOD的外角,
∴∠DOC=∠OAD+∠ODA=62°,
∴∠OAD=∠ODA=31°,
∴∠CDA=∠ODC+∠ODA=90°+31°=121°.
故答案为:121.
点评:本题考查了圆的切线性质,等腰三角形的性质,三角形的内角和定理及外角性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.该题属于几何综合题,在解题时应注意把代数与几何图形的性质及计算与证明有机融合起来,进行分析、推理,从而达到解决问题的目的.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )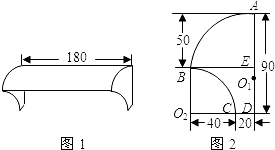 0.1平方米)
0.1平方米)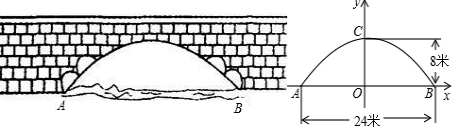
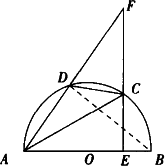
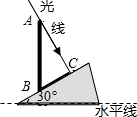 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为